
【题目】某高校随机抽取部分男生测试立定跳远,将成绩整理得到频率分布表如表,测试成绩在220厘米以上(含220厘米)的男生定为“合格生”,成绩在260厘米以上(含260厘米)的男生定为“优良生”.
分组(厘米) | 频数 | 频率 |
[180,200) | 0.10 | |
[200,220) | 15 | |
[220,240) | 0.30 | |
[240,260) | 0.30 | |
[260,280) | 0.20 | |
合计 | 1.00 |
(1)求参加测试的男生中“合格生”的人数.
(2)从参加测试的“合格生”中,根据表中分组情况,按分层抽样的方法抽取8名男生,再从这8名男生中抽取3名男生,记X表示3人中“优良生”的人数,求X的分布列及数学期望.
【答案】(1)120人(2)分布列见解析,数学期望![]() .
.
【解析】
(1)利用频率分布直方图求出第2小组的频率,由此能求出总人数和不是“合格生”的人数,从而能求出参加测试的男生中“合格生”的人数;(2)在“合格生”中根据分层抽样,有各组中抽取的人数分别为3人,3人,2人,其中,“优良生”有2人,![]() 的可能取值为0,1,2,由此能求出
的可能取值为0,1,2,由此能求出![]() 的分布列和数学期望.
的分布列和数学期望.
(1)第2小组的频率为:1-(0.10+0.30+0.30+0.20)=0.10,
∴总人数为![]() 150,
150,
∴不是“合格生”的人数为:0.10×150+0.10×150=30.
∴参加测试的男生中“合格生”的人数为:150﹣30=120.
(2)在“合格生”中根据分层抽样,有各组中抽取的人数分别为3人,3人,2人,
其中,“优良生”有2人,∴X的可能取值为0,1,2,
P(X=0)![]() ,
,
P(X=1)![]() ,
,
P(X=2)![]() ,
,
∴X的分布列为:
X | 0 | 1 | 3 |
P |
|
|
|
EX![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】古希腊著名数学家阿波罗尼斯与欧几里得、阿基米德齐名.他发现:“平面内到两个定点![]() ,
,![]() 的距离之比为定值
的距离之比为定值![]() 的点的轨迹是圆”.后来,人们将这个圆以他的名字命名,称为阿波罗尼斯圆,简称阿氏圆.在平面直角坐标系
的点的轨迹是圆”.后来,人们将这个圆以他的名字命名,称为阿波罗尼斯圆,简称阿氏圆.在平面直角坐标系![]() 中,
中,![]() ,
,![]() ,点
,点![]() 满足
满足![]() .设点
.设点![]() 的轨迹为
的轨迹为![]() ,下列结论正确的是( )
,下列结论正确的是( )
A.![]() 的方程为
的方程为![]()
B.在![]() 上存在点
上存在点![]() ,使得
,使得![]()
C.当![]() ,
,![]() ,
,![]() 三点不共线时,射线
三点不共线时,射线![]() 是
是![]() 的平分线
的平分线
D.在三棱锥中![]() ,
,![]() 面
面![]() ,且
,且![]() ,
,![]() ,
,![]() ,该三棱锥体积最大值为12
,该三棱锥体积最大值为12
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 的焦点
的焦点![]() 恰好是椭圆
恰好是椭圆![]() 的右焦点.
的右焦点.
(1)求实数![]() 的值及抛物线
的值及抛物线![]() 的准线方程;
的准线方程;
(2)过点![]() 任作两条互相垂直的直线分别交抛物线
任作两条互相垂直的直线分别交抛物线![]() 于
于![]() 、
、![]() 和
和![]() 、
、![]() 点,求两条弦的弦长之和
点,求两条弦的弦长之和![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在底面为正方形的四棱锥P—ABCD中,AB=2,PA=4,PB=PD=![]() ,AC与BD相交于点O,E,G分别为PD,CD中点,
,AC与BD相交于点O,E,G分别为PD,CD中点,
(1)求证:EO//平面PBC;
(2)设线段BC上点F满足BC=3BF,求三棱锥E—OFG的体积.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在三棱锥P﹣ABC中,AB=1,BC=2,AC![]() ,PC
,PC![]() ,PA
,PA![]() ,PB
,PB![]() ,E是线段BC的中点.
,E是线段BC的中点.
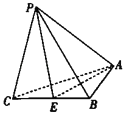
(1)求点C到平面APE的距离d;
(2)求二面角P﹣EA﹣B的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点P为椭圆C:![]() 1(a>b>0)上一点,F1,F2分别是椭圆C的左、右两个焦点,|PF1|=2|PF2|,且cos∠F1PF2
1(a>b>0)上一点,F1,F2分别是椭圆C的左、右两个焦点,|PF1|=2|PF2|,且cos∠F1PF2![]() ,过点F2且斜率为k的直线l与椭圆C交于A,B两点.
,过点F2且斜率为k的直线l与椭圆C交于A,B两点.
(1)求椭圆C的离心率;
(2)若点M(1,![]() )在C上,求△MAB面积的最大值.
)在C上,求△MAB面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,已知△ABC三个顶点坐标为A(7,8),B(10,4),C(2,-4).
(1)求BC边上的中线所在直线的方程;
(2)求BC边上的高所在直线的方程.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】试题分析:(1)根据中点坐标公式求出![]() 中点
中点![]() 的坐标,根据斜率公式可求得
的坐标,根据斜率公式可求得![]() 的斜率,利用点斜式可求
的斜率,利用点斜式可求![]() 边上的中线所在直线的方程;(2)先根据斜率公式求出
边上的中线所在直线的方程;(2)先根据斜率公式求出![]() 的斜率,从而求出
的斜率,从而求出![]() 边上的高所在直线的斜率为
边上的高所在直线的斜率为![]() ,利用点斜式可求
,利用点斜式可求![]() 边上的高所在直线的方程.
边上的高所在直线的方程.
试题解析:(1)由B(10,4),C(2,-4),得BC中点D的坐标为(6,0),
所以AD的斜率为k=![]() =8,
=8,
所以BC边上的中线AD所在直线的方程为y-0=8(x-6),
即8x-y-48=0.
(2)由B(10,4),C(2,-4),得BC所在直线的斜率为k=![]() =1,
=1,
所以BC边上的高所在直线的斜率为-1,
所以BC边上的高所在直线的方程为y-8=-(x-7),即x+y-15=0.
【题型】解答题
【结束】
17
【题目】已知直线l:x-2y+2m-2=0.
(1)求过点(2,3)且与直线l垂直的直线的方程;
(2)若直线l与两坐标轴所围成的三角形的面积大于4,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在如图所示的五面体ABCDEF中,AB∥CD,AB=2AD=2,∠ADC=∠BCD=120°,四边形EDCF是正方形,二面角E﹣DC﹣A的大小为90°.
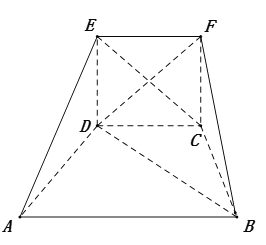
(1)求证:直线AD⊥平面BDE
(2)求点D到平面ABE的距离.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com