
如图,在长方体![]() 中,
中,![]() ,
,![]() ,点E在棱AB上移动,小蚂蚁从点A沿长方体的表面爬到点
,点E在棱AB上移动,小蚂蚁从点A沿长方体的表面爬到点![]() ,所爬的最短路程为
,所爬的最短路程为![]() 。
。

(1)求证:![]() ;
;
(2)求AB的长度;
(3)在线段AB上是否存在点E,使得二面角![]() 的大小为
的大小为![]() ?若存在,确定点E的位置;若不存在,请说明理由。
?若存在,确定点E的位置;若不存在,请说明理由。
解:
解法一:
(1)连接![]() ,由长方体的性质可知:
,由长方体的性质可知:
AE⊥平面![]() ,
,
∴![]() 是
是![]() 在平面
在平面![]() 内的射影。
内的射影。
又∵![]() ,∴四边形
,∴四边形![]() 是正方形,∴
是正方形,∴![]() ,
,
∴![]() (三垂线定理)。
(三垂线定理)。
(2)设![]() ,∵四边形
,∵四边形![]() 是正方形,
是正方形,
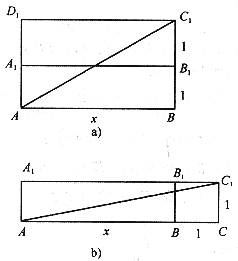
∴ 小蚂蚁从点A沿长方体的表面爬到点![]() 可能有两种途径:
可能有两种途径:
如图a的最短路程为![]()
如图b的最短路程为![]()
∵![]()
∴![]()
∴![]() ,∴
,∴![]()
(3)假设存在点E,连接DE,设![]() ,过点D在
,过点D在
平面ABCD内作DH⊥EC,连接![]() ,则
,则![]() 为二面角
为二面角![]() 的平面角,
的平面角,
∴![]() ;
;
∴![]()
在![]() 内,
内,![]() ,而
,而![]()
即![]() ,解得
,解得![]() 。
。
即存在点E,且到点B的距离为![]() 时,二面角
时,二面角![]() 的大小为
的大小为![]() 。
。
解法二:
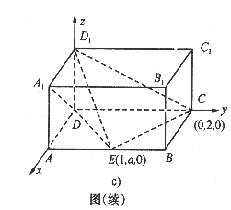
(1)如图c建立空间坐标系,设![]()
则![]()
∴![]()
∴![]() 。
。
(2)同解法一。
(3)假设存在点E,平面DEC的法向量![]()
设平面![]() 的法向量
的法向量![]() ,则
,则
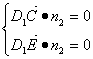 ,即
,即![]()
解得![]() ,∴
,∴![]()
由题意得,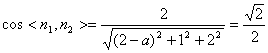
解得![]() 或
或![]() (舍去)
(舍去)
即当点E离B为![]() 时,二面角
时,二面角![]() 的大小为
的大小为![]() 。
。


 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案科目:高中数学 来源: 题型:
(08年惠州一中四模理) 如图,在长方体![]() 中,
中,![]() ,点E在棱
,点E在棱![]() 上移动。
上移动。
(Ⅰ)证明:![]() ;
;
(Ⅱ)当E为![]() 的中点时,求点E到面
的中点时,求点E到面![]() 的距离;
的距离;
(Ⅲ)![]() 等于何值时,二面角
等于何值时,二面角![]() 的大小为
的大小为![]() 。
。

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com