练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    解答题：

    (理)已知A、B、C为△ABC的三个内角，设

    ．

    (1)

    当f(A，B)取得最小值时，求C的大小；

    (2)

    当时，记h(A)＝f(A，B)，试求h(A)的表达式及定义域；

    (3)

    在(2)的条件下，是否存在向量p，使得函数h(A)的图象按向量p平移后得

    到函数的图象？若存在，求出向量p的坐标；若不存在，请说明

    理由．

    答案：
    解析：

    (1)

    解：配方得f(A，B)＝(sin2A－)2＋(cos2B－)2＋1，

    ∴[f(A，B)]min＝1，当且仅当时取得最小值．

    在△ABC中，故C＝或．

    (2)

    解：A＋B＝，于是

    h(A)＝

    ＝cos2A－＋3＝2cos(2A＋)＋3．∵A＋B＝，∴．

    (3)

    解：∵函数h(A)在区间上是减函数，在区间上是增函数；而函数

    在区间上是减函数．

    ∴函数h(A)的图象与函数的图象不相同，从而不存在满足条件的

    向量p．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：2004全国各省市高考模拟试题汇编(天利38套)·数学 题型：044

    已知函数f(x)的图像与函数h(x)＝x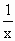＋＋2的图像关于点A(0，1)对称．

    (1)求f(x)的解析式；

    (2)(文)若g(x)＝f(x)·x＋ax，且g(x)在区间(0，2]上为减函数，求实数a的取值范围；

    (理)若g(x)＝f(x)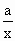＋，且g(x)在区间(0，2]上为减函数，求实数a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源：2004全国各省市高考模拟试题汇编(天利38套)·数学 题型：044

    已知f(x)＝2cos2x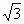＋sin2x＋a(a∈R)

    ①若x∈R，求f(x)的单调增区间

    ②若x∈[0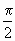，]时，f(x)的最大值为4，求a的值．

    ③(理)在②的条件下，求满足f(x)＝1且x∈[－π，π]的x的集合．

    查看答案和解析>>

    科目：高中数学 来源：2004全国各省市高考模拟试题汇编(天利38套)·数学 题型：044

    已知函数f(x)是定义在R上的偶函数，当x≥0时，f(x)＝－

    (Ⅰ)求当x＜0时，f(x)的解析式；

    (Ⅱ)试确定函数y＝f(x)(x≥0)的单调区间，并证明你的结论；

    (Ⅲ)(理)若x1≥2，且x2≥2

    证明：|f(x1)－f(x2)|＜2．

    查看答案和解析>>

    科目：高中数学 来源：2004全国各省市高考模拟试题汇编(天利38套)·数学 题型：044

    对于函数f(x)，若存在x0∈R，使f(x0)＝x0成立，则称点(x0，x0)为函数f(x)的不动点．

    (Ⅰ)已知函数f(x)＝ax2＋bx－b(a≠0)有不动点(1，1)和(－3，－3)，求a、b的值；

    (Ⅱ)若对于任意实数b，函数f(x)＝ax2＋bx－b总有两个相异的不动点，求实数a的取值范围；

    (Ⅲ)(理)若定义在实数集R上的奇函数g(x)存在(有限的)n个不动点，求证：n必为奇数．

    查看答案和解析>>

    科目：高中数学 来源：2004全国各省市高考模拟试题汇编(天利38套)·数学 题型：044

    已知f(x)是定义在[－1，1]上的奇函数．当a，b∈[－1，1]，且a＋b≠0时，有＞0．

    (Ⅰ)判断函数f(x)的单调性，并给以证明；

    (Ⅱ)(理)若f(1)＝1且f(x)≤m2－2bm＋1对所有x∈[－1，1]，b∈[－1，1]恒成立，求实数m的取值范围．

    查看答案和解析>>

    同步练习册答案