
【题目】某校从高二年级学生中随机抽取100名学生,将他们某次考试的数学成绩(均为整数)分成六段:[40,50),[50,60),…,[90,100]后得到频率分布直方图(如图所示),
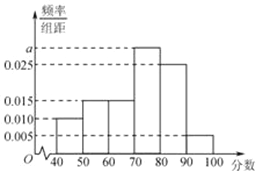
(1)求分数在[70,80)中的人数;
(2)若用分层抽样的方法从分数在[40,50)和[50,60)的学生中共抽取5 人,该5 人中成绩在[40,50)的有几人?
(3)在(2)中抽取的5人中,随机选取2 人,求分数在[40,50)和[50,60)各1 人的概率.
【答案】(1)30;(2)2;(3)![]()
【解析】
(1)由频率分布直方图先求出分数在[70,80)内的概率,由此能求出分数在[70,80)中的人数.
(2)分数在[40,50)的学生有10人,分数在[50,60)的学生有15人,由此能求出用分层抽样的方法从分数在[40,50)和[50,60)的学生中共抽取5 人,抽取的5人中分数在[40,50)的人数.
(3)用分层抽样的方法从分数在[40,50)和[50,60)的学生中共抽取5 人,抽取的5人中分数在[40,50)的有2人分数在[50,60)的有3人,由此利用等可能事件概率计算公式能求出分数在[40,50)和[50,60)各1 人的概率.
(1)由频率分布直方图知小长方形面积为对应区间概率,
所有小长方形面积和为1,因此分数在[70,80)内的概率为:
1﹣(0.005+0.010+0.015×2+0.025)×10=0.3,
∴分数在[70,80)中的人数为:0.3×100=30人.
(2)分数在[40,50)的学生有:0.010×10×100=10人,
分数在[50,60)的学生有:0.015×10×100=15人,
用分层抽样的方法从分数在[40,50)和[50,60)的学生中共抽取5 人,
抽取的5人中分数在[40,50)的人有: ![]()
(3)分数在[40,50)的学生有10人,分数在[50,60)的学生有15人,
用分层抽样的方法从分数在[40,50)和[50,60)的学生中共抽取5 人,
抽取的5人中分数在[40,50)的有2人,设为![]() ,
,![]()
分数在[50,60)的有3人,设为![]() ,
,![]() ,
,![]()
5人中随机抽取2 人共有n=10种可能,它们是:
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
, ![]() ,
,![]()
分别在不同区间上有m=6种可能.![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()
所以分数在[40,50)和[50,60)各1 人的概率P=![]() =
=![]() .
.


 寒假学与练系列答案
寒假学与练系列答案科目:高中数学 来源: 题型:
【题目】已知A,B两地相距24km.甲车、乙车先后从A地出发匀速驶向B地.甲车从A地到B地需行驶25min;乙车从A地到B地需行驶20min.乙车比甲车晚出发2min.
(1)分别写出甲、乙两车所行路程关于甲车行驶时间的函数关系式;
(2)甲、乙两车何时在途中相遇?相遇时距A地多远?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设α,β为两个不同平面,a,b为两条不同直线,下列选项正确的是( )
①若a∥α,b∥α,则a∥b
②若aα,α∥β,则a∥β
③若α∥β,a∥β,则![]()
④若a∥α,则a与平面α内的无数条直线平行
⑤若a∥b,则a平行于经过b的所有平面
A.①②B.③④C.②④D.②⑤
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}和{bn}满足,a1=2,b1=1,且对任意正整数n恒满足2an+1=4an+2bn+1,2bn+1=2an+4bn﹣1.
(1)求证:{an+bn}为等比数列,{an﹣bn}为等差列;
(2)求证![]() (n>1).
(n>1).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,某几何体的三视图中,俯视图是边长为2的正三角形,正视图和左视图分别为直角梯形和直角三角形,则该几何体的体积为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《汉字听写大会》不断创收视新高,为了避免“书写危机”,弘扬传统文化,某市大约10万名市民进行了汉字听写测试.现从某社区居民中随机抽取50名市民的听写测试情况.发现被测试市民正确书写汉字的个数全部在160到184之间,将测试结果按如下方式分成六组:第1组![]() ,第2组
,第2组![]() ,…,第6组
,…,第6组![]() ,如图是按上述分组方法得到的频率分布直方图.
,如图是按上述分组方法得到的频率分布直方图.

(1)试估计该市市民正确书写汉字的个数的平均数与中位数;
(2)已知第4组市民中有3名男性,组织方要从第4组中随机抽取2名市民组成弘扬传统文化宣传队,求至少有1名女性市民的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】数学家欧拉在![]() 年提出定理:三角形的外心、重心、垂心依次位于同一直线上,且重心到外心的距离是重心到垂心距离的一半,这条直线后人称之为三角形的欧拉线.已知
年提出定理:三角形的外心、重心、垂心依次位于同一直线上,且重心到外心的距离是重心到垂心距离的一半,这条直线后人称之为三角形的欧拉线.已知![]() 的顶点
的顶点![]() 、
、![]() ,若其欧拉线方程为
,若其欧拉线方程为![]() ,则顶点
,则顶点![]() 的坐标是( )
的坐标是( )
参考公式:若![]() 的顶点
的顶点![]() 、
、![]() 、
、![]() 的坐标分别是
的坐标分别是![]() 、
、![]() 、
、![]() ,则该
,则该![]() 的重心的坐标为
的重心的坐标为![]() .
.
A.![]() B.
B.![]() ,
,![]()
C.![]() ,
,![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com