
【题目】已知数列{an}满足:a1=﹣13,a6+a8=﹣2,且an﹣1=2an﹣an+1(n≥2),则数列{ ![]() }的前13项和为( )
}的前13项和为( )
A.![]()
B.﹣ ![]()
C.![]()
D.﹣ ![]()
科目:高中数学 来源: 题型:
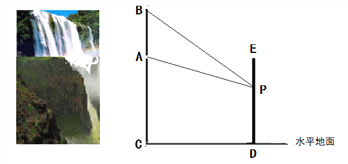
【题目】南京市江北新区计划在一个竖直长度为20米的瀑布![]() 正前方修建一座观光电梯
正前方修建一座观光电梯![]() 。如图所示,瀑布底部
。如图所示,瀑布底部![]() 距离水平地面的高度
距离水平地面的高度![]() 为60米,电梯上设有一个安全拍照口
为60米,电梯上设有一个安全拍照口![]() ,
, ![]() 上升的最大高度为60米。设
上升的最大高度为60米。设![]() 距离水平地面的高度为
距离水平地面的高度为![]() 米,
米, ![]() 处拍照瀑布的视角
处拍照瀑布的视角![]() 为
为![]() 。摄影爱好者发现,要使照片清晰,视角
。摄影爱好者发现,要使照片清晰,视角![]() 不能小于
不能小于![]() 。
。
(1)当![]() 米时,视角
米时,视角![]() 恰好为
恰好为![]() ,求电梯和山脚的水平距离
,求电梯和山脚的水平距离![]() 。
。
(2)要使电梯拍照口![]() 的高度
的高度![]() 在52米及以上时,拍出的照片均清晰,请求出电梯和山脚的水平距离
在52米及以上时,拍出的照片均清晰,请求出电梯和山脚的水平距离![]() 的取值范围。
的取值范围。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对一批共50件的某电器进行分类检测,其重量(克)统计如下:
质量段 | [80,85) | [85,90) | [90,95) | [95,100] |
件数 | 5 | a | 15 | b |
规定重量在82克及以下的为“A”型,重量在85克及以上的为“B”型,已知该批电器有“A“型2件
(1)从该批电器中任选1件,求其为“B”型的概率;
(2)从重量在[80,85)的5件电器中,任选2件,求其中恰有1件为“A”型的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系中,以原点为极点, ![]() 轴的正半轴为极轴,以相同的长度单位建立极坐标系.已知直线的极坐标方程为
轴的正半轴为极轴,以相同的长度单位建立极坐标系.已知直线的极坐标方程为![]() ,曲线
,曲线![]() 的极坐标方程为
的极坐标方程为![]() (
(![]() ).
).
(Ⅰ)设![]() 为参数,若
为参数,若![]() ,求直线
,求直线![]() 的参数方程;
的参数方程;
(Ⅱ)已知直线![]() 与曲线
与曲线![]() 交于
交于![]() ,
, ![]() ,设
,设![]() ,且
,且![]() ,求实数
,求实数![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知△ABC的三个内角A,B,C所对的边分别为a,b,c,∠A是锐角,且 ![]() b=2asinB.
b=2asinB.
(1)求∠A的度数;
(2)若a=7,△ABC的面积为10 ![]() ,求b2+c2的值.
,求b2+c2的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设数列{an}的前n项和为Sn=2n2 , {bn}为等比数列,且a1=b1 , b2(a2﹣a1)=b1 .
(1)求数列{an}和{bn}的通项公式;
(2)设cn= ![]() ,求数列{cn}的前n项和Tn .
,求数列{cn}的前n项和Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】△ABC中内角A,B,C的对边分别为a,b,c,向量 ![]() =(2sinB,﹣
=(2sinB,﹣ ![]() ),
), ![]() =(cos2B,2cos2
=(cos2B,2cos2 ![]() ﹣1)且
﹣1)且 ![]() ∥
∥ ![]() .
.
(1)求锐角B的大小;
(2)如果b=2,求△ABC的面积S△ABC的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,角A,B,C的对边分别为a,b,c,已知a+b=5,c= ![]() ,且4sin2
,且4sin2 ![]() ﹣cos2C=
﹣cos2C= ![]()
(1)求角C的大小;
(2)求△ABC的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com