
分析 (Ⅰ)求出函数的导数,计算f(0),f′(0),从而求出切线方程即可;
(Ⅱ)求出函数的导数,通过讨论a的范围,求出函数的单调区间,得到关于a的不等式组,求出a的范围即可;
(Ⅲ)令h(x)=f(x)+x-a=x3+(1-3a)x-a,等价于函数h(x)在[-a,0]上恰有两个零点,根据函数的单调性求出a的最小值即可.
解答 解:(Ⅰ)因为f'(x)=3(x2-a),所以f'(0)=-3a,
因为f(0)=0,
所以曲线y=f(x)在点(0,f(0))处的切线方程为y=-3ax.…(4分)
(Ⅱ)因为f'(x)=3(x2-a),所以,
当a≤0时,f'(x)≥0在R上恒成立,
所以f(x)在R上单调递增,f(x)没有极值点,不符合题意;…(5分)
当a>0时,令f'(x)=0得$x=±\sqrt{a}$,
当x变化时,f'(x)与f(x)的变化情况如下表所示:
| x | (-∞,$-\sqrt{a}$) | $-\sqrt{a}$ | ($-\sqrt{a}$,$\sqrt{a}$) | $\sqrt{a}$ | ($\sqrt{a}$,+∞) |
| f'(x) | + | 0 | - | 0 | + |
| f(x) | ↗ | 极大值 | ↘ | 极小值 | ↗ |
点评 本题考查了切线方程问题,考查函数的单调性、最值问题,考查导数的应用,是一道综合题.


 一本好题口算题卡系列答案
一本好题口算题卡系列答案科目:高中数学 来源: 题型:解答题
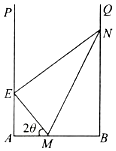 某地拟在一个U形水面PABQ(∠A=∠B=90°)上修一条堤坝(E在AP上,N在BQ上),围出一个封闭区域EABN,用以种植水生植物.为了美观起见,决定从AB上点M处分别向点E,N拉2条分割线ME,MN,将所围区域分成3个部分(如图),每部分种植不同的水生植物.已知AB=a,EM=BM,∠MEN=90°,设所拉分割线总长度为l.
某地拟在一个U形水面PABQ(∠A=∠B=90°)上修一条堤坝(E在AP上,N在BQ上),围出一个封闭区域EABN,用以种植水生植物.为了美观起见,决定从AB上点M处分别向点E,N拉2条分割线ME,MN,将所围区域分成3个部分(如图),每部分种植不同的水生植物.已知AB=a,EM=BM,∠MEN=90°,设所拉分割线总长度为l.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
| 节 气 | 冬至 | 小寒 (大雪) | 大寒 (小雪) | 立春 (立冬) | 雨水 (霜降) | 惊蛰 (寒露) | 春分 (秋分) | 清明 (白露) | 谷雨 (处暑) | 立夏 (立秋) | 小满 (大暑) | 芒种 (小暑) | 夏至 |
| 晷影 长 (寸) | 135.0 | $125.\frac{5}{6}$ | $115.1\frac{4}{6}$ | $105.2\frac{3}{6}$ | $95.3\frac{2}{6}$ | $85.4\frac{2}{6}$ | 75.5 | $66.5\frac{5}{6}$ | $55.6\frac{4}{6}$ | $45.7\frac{3}{6}$ | $35.8\frac{2}{6}$ | $25.9\frac{1}{6}$ | 16.0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | $\frac{1}{8}$ | B. | $\frac{3}{8}$ | C. | $\frac{7}{8}$ | D. | $\frac{1}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $[\frac{{3\sqrt{2}}}{2},\sqrt{5}]$ | B. | $[\frac{{3\sqrt{2}}}{2},5]$ | C. | $[\frac{9}{2},5]$ | D. | $[\sqrt{5},\frac{9}{2}]$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|x>2} | B. | {x|1<x≤2} | C. | {x|1≤x<2} | D. | {x|x≤2} |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com