
【题目】已知数列{an}的前n项和为Sn , Sn=n2+n.
(Ⅰ)求{an}的通项公式an;
(Ⅱ)若ak+1 , a2k , a2k+3(k∈N*)恰好依次为等比数列{bn}的第一、第二、第三项,求数列{ ![]() }的前n项和Tn .
}的前n项和Tn .
【答案】解:(Ⅰ)当n=1时,a1=S1=2.当n≥2时,an=Sn﹣Sn﹣1=(n2+n)﹣[(n﹣1)2+(n﹣1)]=2n.
检验n=1时,上式符合.
∴an=2n..
(Ⅱ)由题知:ak+1 , a2k , a2k+3(k∈N*)恰好依次为等比数列{bn}的第一、第二、第三项,
∴ ![]() =ak+1a2k+3(k∈N*),
=ak+1a2k+3(k∈N*),
即(2×2k)2=2(k+1)2(2k+3),解得k=3.
∴b1=a4=8,b2=a6=12,公比q= ![]() =
= ![]() .
.
∴bn= ![]() ,
,
∴ ![]() =
= ![]() ,
,
∴Tn= ![]()
![]() +
+ ![]() +…+
+…+ 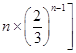 .
.![]() =
= 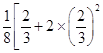 +…+
+…+ 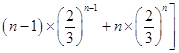 ,
,
∴ ![]() =
= 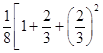 +…+
+…+ 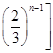 ﹣
﹣ ![]() =
= ![]() ﹣
﹣ ![]() ×
× ![]() ,
,
Tn= ![]() ﹣
﹣ ![]() ×
× ![]() .
.
【解析】(Ⅰ)当n=1时,a1=S1=2.当n≥2时,an=Sn﹣Sn﹣1 , 即可得出.(Ⅱ)由题知:ak+1 , a2k , a2k+3(k∈N*)恰好依次为等比数列{bn}的第一、第二、第三项,可得 ![]() =ak+1a2k+3(k∈N*),解得k=3.可得bn=
=ak+1a2k+3(k∈N*),解得k=3.可得bn= ![]() ,
, ![]() =
= ![]() ,再利用“错位相减法”与求和公式即可得出.
,再利用“错位相减法”与求和公式即可得出.
【考点精析】掌握数列的前n项和是解答本题的根本,需要知道数列{an}的前n项和sn与通项an的关系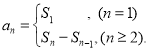 .
.


 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案科目:高中数学 来源: 题型:
【题目】2018年6月19日凌晨某公司公布的年中促销全天交易数据显示,天猫年中促销当天全天下单金额为1592亿元.为了了解网购者一次性购物情况,某统计部门随机抽查了6月18日100名网购者的网购情况,得到如下数据统计表,已知网购金额在2000元以上(不含2000元)的频率为0.4.

网购金额(元) | 频数 | 频率 |
| 5 | 0.05 |
|
|
|
| 15 | 0.15 |
| 25 | 0.25 |
| 30 | 0.3 |
|
|
|
合计 | 100 | 1 |
(Ⅰ)先求出![]() 的值,再将图中所示的频率分布直方图绘制完整;
的值,再将图中所示的频率分布直方图绘制完整;
(Ⅱ)对这100名网购者进一步调查显示:购物金额在2000元以上的购物者中网龄3年以上的有35人,购物金额在2000元以下(含2000元)的购物者中网龄不足3年的有20人,请填写下面的列联表,并据此判断能否在犯错误的概率不超过0.025的前提下认为网购金额超过2000元与网龄在3年以上有关?
网龄3年以上 | 网龄不足3年 | 总计 | |
购物金额在2000元以上 | 35 | ||
购物金额在2000元以下 | 20 | ||
总计 | 100 |
参考数据:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.076 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
参考公式:![]() 其中
其中![]() .
.
(Ⅲ)从这100名网购者中根据购物金额分层抽出20人给予返券奖励,为进一步激发购物热情,在![]() 和
和![]() 两组所抽中的8人中再随机抽取2人各奖励1000元现金,求
两组所抽中的8人中再随机抽取2人各奖励1000元现金,求![]() 组获得现金奖的数学期望.
组获得现金奖的数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)满足 ![]() ,当
,当 ![]() 时,f(x)=lnx,若在
时,f(x)=lnx,若在 ![]() 上,方程f(x)=kx有三个不同的实根,则实数k的取值范围是( )
上,方程f(x)=kx有三个不同的实根,则实数k的取值范围是( )
A.![]()
B.[﹣4ln4,﹣ln4]
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知某单位甲、乙、丙三个部门的员工人数分别为24,16,16.现采用分层抽样的方法从中抽取7人,进行睡眠时间的调查.
(1)应从甲、乙、丙三个部门的员工中分别抽取多少人?
(2)若抽出的7人中有4人睡眠不足,3人睡眠充足,现从这7人中随机抽取3人做进一步的身体检查.用X表示抽取的3人中睡眠不足的员工人数,求随机变量X的分布列与数学期望;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】按下列要求分配6本不同的书,各有多少种不同的分配方式?
(1)分成三份,1份1本,1份2本,1份3本;
(2)甲、乙、丙三人中,一人得1本,一人得2本,一人得3本;
(3)平均分成三份,每份2本;
(4)平均分配给甲、乙、丙三人,每人2本;
(5)分成三份,1份4本,另外两份每份1本;
(6)甲、乙、丙三人中,一人得4本,另外两人每人得1本;
(7)甲得1本,乙得1本,丙得4本.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 是正方形,其他四个侧面都是等边三角形,
是正方形,其他四个侧面都是等边三角形,![]() 与
与![]() 的交点为
的交点为![]() ,
,![]() 为侧棱
为侧棱![]() 上一点.
上一点.

(Ⅰ)求证:平面![]() 平面
平面![]() ;
;
(Ⅱ)当二面角![]() 的大小为
的大小为![]() 时,
时,
试判断点![]() 在
在![]() 上的位置,并说明理由.
上的位置,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有人在路边设局,宣传牌上写有“掷骰子,赢大奖”.其游戏规则是这样的:你可以在1,2,3,4,5,6点中任选一个,并押上赌注![]() 元,然后掷1颗骰子,连续掷3次,若你所押的点数在3次掷骰子过程中出现1次,2次,3次,那么原来的赌注仍还给你,并且庄家分别给予你所押赌注的1倍,2倍,3倍的奖励.如果3次掷骰子过程中,你所押的点数没出现,那么你的赌注就被庄家没收.
元,然后掷1颗骰子,连续掷3次,若你所押的点数在3次掷骰子过程中出现1次,2次,3次,那么原来的赌注仍还给你,并且庄家分别给予你所押赌注的1倍,2倍,3倍的奖励.如果3次掷骰子过程中,你所押的点数没出现,那么你的赌注就被庄家没收.
(1)求掷3次骰子,至少出现1次为5点的概率;
(2)如果你打算尝试一次,请计算一下你获利的期望值,并给大家一个正确的建议.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知a,b,c分别是△ABC内角A,B,C的对边,且 ![]() csinA=acosC.
csinA=acosC.
(I)求C的值;
(Ⅱ)若c=2a,b=2 ![]() ,求△ABC的面积.
,求△ABC的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com