
分析 由奇偶性的定义来判断①,由分类讨论结合反比例函数的单调性求解②;由②结合①对称区间上的单调性相同说明③正确;由数形结合来说明④不正确.
解答 解:①f(-x)=$\frac{-x}{1+|-x|}$=-f(x),∴函数是奇函数,正确
②当x>0时,f(x)=$\frac{1}{1+\frac{1}{x}}$∈(0,1)
由①知当x<0时,f(x)∈(-1,0),x=0时,f(x)=0
∴f(x)∈(-1,1)正确;
③则当x>0时,f(x)=$\frac{1}{1+\frac{1}{x}}$反比例函数的单调性可知,f(x)在(0,+∞)上是增函数
再由①知f(x)在(-∞,0)上也是增函数,正确
④由③知f(x)的图象与y=x只有(0,0)这一个交点.不正确.
故答案为:①②③.
点评 本题考查函数的定义域,单调性,奇偶性,值域,考查全面,方法灵活,这四个问题在研究时往往是同时考虑的.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
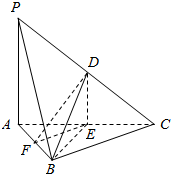 如图所示,在三棱锥P-ABC中,D,E,F分别为棱PC,AC,AB的中点.已知PA⊥AC,PA=6,BC=8,DF=5.
如图所示,在三棱锥P-ABC中,D,E,F分别为棱PC,AC,AB的中点.已知PA⊥AC,PA=6,BC=8,DF=5.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ($\frac{1}{2}$,1) | B. | (0,$\frac{1}{2}$)∪(1,+∞) | C. | ($\frac{1}{2}$,2) | D. | (0,1)∪(2,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-2,1) | B. | ( 2,1) | C. | (-2,3) | D. | (2,3) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 既不充分也不必要条件 | ||
| C. | 充要条件 | D. | 必要不充分条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
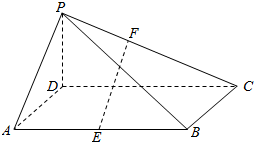 在如图所示的四棱锥中,底面ABCD是平行四边形,AB=4,BC=2,∠BCD=60°,且PD⊥底面ABCD,点E是AB的中点,点F是PC上一点.
在如图所示的四棱锥中,底面ABCD是平行四边形,AB=4,BC=2,∠BCD=60°,且PD⊥底面ABCD,点E是AB的中点,点F是PC上一点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com