
【题目】某电子商务平台的管理员随机抽取了1000位上网购物者,并对其年龄(在10岁到69岁之间)进行了调查,统计情况如下表所示.
年龄 |
|
|
|
|
|
|
人数 | 100 | 150 |
| 200 |
| 50 |
已知![]() ,
,![]() ,
,![]() 三个年龄段的上网购物的人数依次构成递减的等比数列.
三个年龄段的上网购物的人数依次构成递减的等比数列.
(1)求![]() 的值;
的值;
(2)若将年龄在![]() 内的上网购物者定义为“消费主力军”,其他年龄段内的上网购物者定义为“消费潜力军”.现采用分层抽样的方式从参与调查的1000位上网购物者中抽取5人,再从这5人中抽取2人,求这2人中至少有一人是消费潜力军的概率.
内的上网购物者定义为“消费主力军”,其他年龄段内的上网购物者定义为“消费潜力军”.现采用分层抽样的方式从参与调查的1000位上网购物者中抽取5人,再从这5人中抽取2人,求这2人中至少有一人是消费潜力军的概率.
科目:高中数学 来源: 题型:
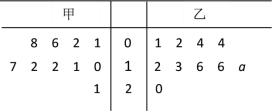
【题目】为培养学生的阅读习惯,某校开展了为期一年的“弘扬传统文化,阅读经典名著”活动. 活动后,为了解阅读情况,学校统计了甲、乙两组各10名学生的阅读量(单位:本),统计结果用茎叶图记录如下,乙组记录中有一个数据模糊,无法确认,在图中以a表示.
(Ⅰ)若甲组阅读量的平均值大于乙组阅读量的平均值, 求图中a的所有可能取值;
(Ⅱ)将甲、乙两组中阅读量超过15本的学生称为“阅读达人”. 设![]() ,现从所有“阅读达人”里任取3人,求其中乙组的人数X的分布列和数学期望.
,现从所有“阅读达人”里任取3人,求其中乙组的人数X的分布列和数学期望.
(Ⅲ)记甲组阅读量的方差为![]() . 在甲组中增加一名学生A得到新的甲组,若A的阅读量为10,则记新甲组阅读量的方差为
. 在甲组中增加一名学生A得到新的甲组,若A的阅读量为10,则记新甲组阅读量的方差为![]() ;若A的阅读量为20,则记新甲组阅读量的方差为
;若A的阅读量为20,则记新甲组阅读量的方差为![]() ,试比较
,试比较![]() ,
,![]() ,
,![]() 的大小.(结论不要求证明)
的大小.(结论不要求证明)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(2017高考新课标Ⅲ,理19)如图,四面体ABCD中,△ABC是正三角形,△ACD是直角三角形,∠ABD=∠CBD,AB=BD.

(1)证明:平面ACD⊥平面ABC;
(2)过AC的平面交BD于点E,若平面AEC把四面体ABCD分成体积相等的两部分,求二面角D–AE–C的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学为了组建一支业余足球队,在高一年级随机选取50名男生测量身高,发现被测男生的身高全部在![]() 到
到![]() 之间,将测量结果按如下方式分成六组:第1组
之间,将测量结果按如下方式分成六组:第1组![]() ,第2组
,第2组![]() ,…,第6组
,…,第6组![]() ,如图是按上述分组得到的频率分布直方图,以频率近似概率.
,如图是按上述分组得到的频率分布直方图,以频率近似概率.
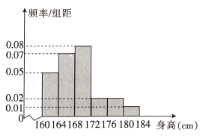
(1)若学校要从中选1名男生担任足球队长,求被选取的男生恰好在第5组或第6组的概率;
(2)试估计该校高一年级全体男生身高的平均数(同一组中的数据用该组区间的中点值代表)与中位数;
(3)现在从第5与第6组男生中选取两名同学担任守门员,求选取的两人中最多有1名男生来自第5组的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国古代数学家祖暅提出原理:“幂势既同,则积不容异”.其中“幂”是截面积,“势”是几何体的高.该原理的意思是:夹在两个平行平面间的两个几何体,被任一平行于这两个平行平面的平面所截,若所截的两个截面的面积恒相等,则这两个几何体的体积相等.如图,在空间直角坐标系中的![]() 平面内,若函数
平面内,若函数![]() 的图象与
的图象与![]() 轴围成一个封闭的区域
轴围成一个封闭的区域![]() ,将区域
,将区域![]() 沿
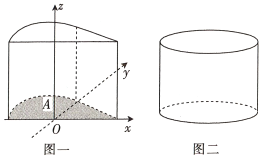
沿![]() 轴的正方向平移8个单位长度,得到几何体如图一,现有一个与之等高的圆柱如图二,其底面积与区域
轴的正方向平移8个单位长度,得到几何体如图一,现有一个与之等高的圆柱如图二,其底面积与区域![]() 的面积相等,则此圆柱的体积为__________.
的面积相等,则此圆柱的体积为__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,底面ABCD为菱形,∠DAB=60°,PD⊥底面ABCD,PD=DC=2,E,F,G分别是AB,PB,CD的中点.
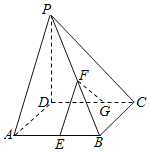
(1)求证:AC⊥PB;
(2)求证:GF∥平面PAD;
(3)求点G到平面PAB的距离.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com