【题目】已知双曲线
：
的左、右焦点分别为
，
，
，
是右支上的一点，
与
轴交于点
，
的内切圆在边
上的切点为
．若
，则的离心率是________．
科目：高中数学 来源： 题型：
【题目】对于给定数列
，若数列
满足：对任意
，都有
，则称数列是数列的“相伴数列”.
（1）若
，且数列是数列的“相伴数列”，试写出
的一个通项公式，并说明理由；
（2）设
，证明：不存在等差数列，使得数列是数列的“相伴数列”；
（3）设
,
（其中
），若是数列的“相伴数列”，试分析实数b、q的取值应满足的条件.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】中国足球甲
联赛共有12个足球俱乐部参加，实行主客场双循环赛制，即任何两队分别在主场和客场各比赛一场，胜一场得3分，平一场各得1分，负一场得0分，在联赛结束后按积分的高低排出名次.则在积分榜上位次相邻的两支球队积分差距最多可达_________分.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数
，
.
（Ⅰ）若
为偶函数，求
的值并写出的增区间；
（Ⅱ）若关于
的不等式
的解集为
，当
时，求
的最小值；
（Ⅲ）对任意的
，
，不等式
恒成立，求实数的取值范围.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】（1）在
中，角A，B，C所对的边分别是a，b，c，证明余弦定理：
；
（2）长江某地南北岸平行，如图所示，江面宽度
，一艘游船从南岸码头A出发航行到北岸，假设游船在静水中的航行速度
，水流速度
，设
和
的夹角为θ（
），北岸的点
在点A的正北方向.
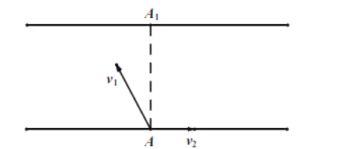
①当
多大时，游船能到达处，需要航行多少时间？
②当
时，判断游船航行到达北岸的位置在的左侧还是右侧，并说明理由.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】
如图，已知椭圆
的离心率为
，以该椭圆上的点和椭圆的左、右焦点
为顶点的三角形的周长为
.一等轴双曲线的顶点是该椭圆的焦点，设
为该双曲线上异于顶点的任一点，直线
和
与椭圆的交点分别为
和
.
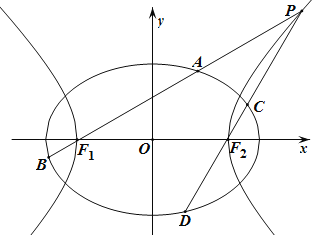
（Ⅰ）求椭圆和双曲线的标准方程；
（Ⅱ）设直线、的斜率分别为
、
，证明
；
（Ⅲ）是否存在常数
，使得
恒成立？若存在，求的值；若不存在，请说明理由.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】在平面直角坐标系
中，直线
与x、y轴分别交于点
、
，记以点
为圆心，半径为r的圆与三角形
的边的交点个数为M.对于下列说法：①当
时，若
，则
；②当
时，若
，则
；③当
时，M不可能等于3；④M的值可以为0，1，2，3，4，5.其中正确的个数为（ ）
A.1B.2C.3D.4
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】现有甲、乙、丙三个盒子，其中每个盒子中都装有标号分别为1、2、3、4、5、6的六张卡片，现从甲、乙、丙三个盒子中依次各取一张卡片使得卡片上的标号恰好成等差数列的取法数为（ ）
A.14B.16C.18D.20
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
