
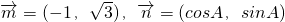 ,且
,且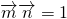 .
.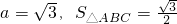 ,求b和c的值.
,求b和c的值.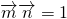 ,得到-cosA+
,得到-cosA+ sinA=1,
sinA=1, sinA-cosA=1,化简得sin(A-
sinA-cosA=1,化简得sin(A- )=
)= ,
, <A-
<A- <
< ,
, =
= ,即A=
,即A= ;
; ,可知
,可知 =
= ,即(b+c)2-a2=3bc①,
,即(b+c)2-a2=3bc①, bcsinA=
bcsinA= ,得bc=2,又a=
,得bc=2,又a= ,
,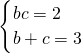 ,解得:
,解得: 或
或 .
.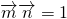 ,然后利用两角正弦函数公式及特殊角的三角函数值化为一个角的正弦函数,根据A的范围求出这个角的范围,利用特殊角的三角函数值求出这个角的度数,进而得到A的度数;
,然后利用两角正弦函数公式及特殊角的三角函数值化为一个角的正弦函数,根据A的范围求出这个角的范围,利用特殊角的三角函数值求出这个角的度数,进而得到A的度数;

 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
| OA |
| OB |
| OC |
| OA |
| OB |
| 1-x |
| ax |
| OC |
| o |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| n |
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
查看答案和解析>>
科目:高中数学 来源:0119 期末题 题型:单选题
 β,则a∥b; ④若a与b异面,且a∥β,则b与β相交;
β,则a∥b; ④若a与b异面,且a∥β,则b与β相交;[ ]
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com