
命题“在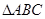 中,若
中,若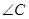 是直角,则
是直角,则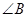 一定是锐角.”的证明过程如下:
一定是锐角.”的证明过程如下:
假设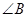 不是锐角,则
不是锐角,则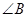 是直角或钝角,即
是直角或钝角,即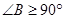 ,而
,而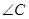 是直角,
是直角,
所以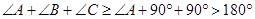 ,
,
这与三角形的内角和等于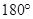 矛盾,所以上述假设不成立,
矛盾,所以上述假设不成立,
即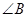 一定是锐角.
一定是锐角.
本题采用的证明方法是( )
A. 综合法 B. 分析法 C. 反证法 D. 数学归纳法
科目:高中数学 来源:2010-2011学年江西省高三上学期期中考试数学理卷 题型:选择题
有下列命题:①在空间中,若 ,
,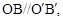 则
则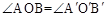 ;②直角梯形是平面图形;③
;②直角梯形是平面图形;③ ; ④若
; ④若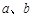 是两条异面直线,
是两条异面直线,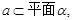
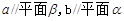 ,则
,则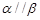 ;⑤在四面体
;⑤在四面体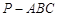 中,
中,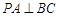 ,
,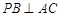 ,则点
,则点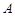 在面
在面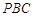 内的射影为
内的射影为 的垂心,其中真命题的个数是( )
的垂心,其中真命题的个数是( )
A.1 B.2 C.3 D.4
查看答案和解析>>
科目:高中数学 来源:2010-2011学年广东省中山市高三第一次月考数学理卷 题型:选择题
命题“在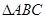 中,若
中,若 是直角,则
是直角,则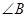 一定是锐角.”的证明过程如下:
一定是锐角.”的证明过程如下:
假设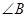 不是锐角,则
不是锐角,则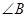 是直角或钝角,即
是直角或钝角,即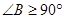 ,而
,而 是直角,
是直角,
所以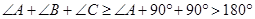 ,
,
这与三角形的内角和等于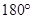 矛盾,所以上述假设不成立,
矛盾,所以上述假设不成立,
即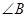 一定是锐角.本题采用的证明方法是
一定是锐角.本题采用的证明方法是
A. 综合法 B. 分析法 C. 反证法 D. 数学归纳法
查看答案和解析>>
科目:高中数学 来源:2010年广东省东莞市高二下学期期末考试(理科)数学卷 题型:选择题
命题“在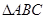 中,若
中,若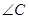 是直角,则
是直角,则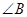 一定是锐角.”的证明
一定是锐角.”的证明 过程如下:
过程如下:
假设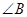 不是锐角,则
不是锐角,则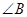 是直角或钝角,即
是直角或钝角,即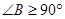 ,而
,而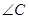 是直角,
是直角,
所以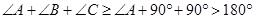 ,
,
这与三角形的内角和等于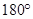 矛盾,所以上述假设不成立,
矛盾,所以上述假设不成立,
即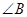 一定是锐角.
一定是锐角.
本题采用的证明方法是
A. 综合法 B. 分析法 C. 反证法 D. 数学归纳法
查看答案和解析>>
科目:高中数学 来源: 题型:
有下列命题:①在空间中,若![]() ,
,![]() 则
则![]() ;②直角梯形是平面图形;③
;②直角梯形是平面图形;③![]() ; ④若
; ④若![]() 是两条异面直线,
是两条异面直线,![]()
![]() ,则
,则![]() ;⑤在四面体
;⑤在四面体![]() 中,
中,![]() ,
,![]() ,则点
,则点![]() 在面
在面![]() 内的射影为
内的射影为![]() 的垂心,其中真命题的个数是( )
的垂心,其中真命题的个数是( )
A.1 B.2 C.3 D.4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com