
����Ŀ��ij��˾Ϊ��ȷ�ذ����г������ò�Ʒ�����ƻ����Թ�ȥ��������ݽ��������õ��˵�![]() ����������
����������![]() (��λ�����)֮��Ĺ�ϵ�����
(��λ�����)֮��Ĺ�ϵ�����


(��)��ͼ�л����������ݵ�ɢ��ͼ��
(��)����(��)�е�ɢ��ͼ���![]() ��
��![]() �Ļع�ģ�ͣ��������ϵ������˵����
�Ļع�ģ�ͣ��������ϵ������˵����
(��)����![]() ����
����![]() �Ļع鷽�̣�Ԥ���5���������ԼΪ���٣�.
�Ļع鷽�̣�Ԥ���5���������ԼΪ���٣�.
��ע���ο����ݣ� 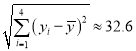 ��
�� ![]() ��
�� ![]() .
.
�ο���ʽ�����ϵ�� ��
��
�ع鷽��![]() ��б�ʺͽؾ����С���˷����ƹ�ʽ�ֱ�Ϊ��
��б�ʺͽؾ����С���˷����ƹ�ʽ�ֱ�Ϊ��
 ��
�� ![]() .
.
���𰸡�(��)ɢ��ͼ��������(��)�𰸼�������(��) 71���.
�����������������
(��) ��������������ɢ��ͼ;
(��) �������ṩ�������빫ʽ���![]() ��
��![]() �����ϵ��r,���ɵó�����;
�����ϵ��r,���ɵó�����;
(��) ���������ṩ������,�ֱ����![]() ��ֵ,��ɵûع�ֱ�߷���,�ٽ�
��ֵ,��ɵûع�ֱ�߷���,�ٽ�![]() ����ع�ֱ�߷��̿ɵý���.
����ع�ֱ�߷��̿ɵý���.
���������
(��)����ɢ��ͼ��ͼ��

(��)��(��)ɢ��ͼ��֪��������·ֲ���һ��ֱ�߸������������������ο����ݵã�
![]() ��
�� ![]() ��
�� ![]() ��
��  ��
�� ![]() ��
�� ![]() ��
��  ��
��
 .
.
��![]() ��
��![]() �����ϵ������Ϊ0.9996��˵��
�����ϵ������Ϊ0.9996��˵��![]() ��
��![]() ��������س̶��൱��
��������س̶��൱��
����������Իع�ģ�����![]() ��
��![]() �Ĺ�ϵ.
�Ĺ�ϵ.
(��)��(��)֪�� ![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() ��
��
 ��
�� ![]() ��
��
��![]() ����
����![]() �Ļع�ֱ�߷���Ϊ
�Ļع�ֱ�߷���Ϊ![]() ��
��
��![]() ʱ��
ʱ�� ![]() ��
��
���Ե�5���������ԼΪ71���.


 ��������ܸ�ϰϵ�д�
��������ܸ�ϰϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������{an}����a1=1�� ![]() ��n��N+����
��n��N+����
��1��֤�������� ![]() �ǵȲ����У�
�ǵȲ����У�
��2��������{an}��ͨ�ʽan��
��3����bn=n��n+1��an �� ������{bn}��ǰn���Sn ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����13�֣���ͼ����Բ![]() ������
������![]() ��������
��������![]() ��ֱ��l�ķ���Ϊ
��ֱ��l�ķ���Ϊ![]() ��
��

��1������ԲC�ķ��̣�
��2��![]() �Ǿ����ҽ���
�Ǿ����ҽ���![]() ����һ�ң���������
����һ�ң���������![]() ������ֱ��
������ֱ��![]() ��ֱ��
��ֱ��![]() �ཻ�ڵ�
�ཻ�ڵ�![]() ����
����![]() ��
��![]() ��
��![]() ��б�ʷֱ�Ϊ
��б�ʷֱ�Ϊ![]() ��
��![]() ��
��![]() ���ʣ��Ƿ���ڳ���
���ʣ��Ƿ���ڳ���![]() ��ʹ��
��ʹ��![]() ? �����ڣ���
? �����ڣ���![]() ��ֵ�� �������ڣ���˵�����ɣ�
��ֵ�� �������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ֱ֪��l������P����2��5������б��Ϊ�� ![]()
��1����ֱ��l�ķ��̣�
��2����ֱ��m��lƽ�У��ҵ�P��ֱ��m�ľ���Ϊ3����ֱ��m�ķ��̣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�����̴����ˮ����ֳ������һ��С��Ϻ���������ȡ40ֻ����ͳ�ƣ�����������ͳ�ƽ������ͼ��

��1�����¼�![]() Ϊ����������С��Ϻ����ȡһֻ������������35
Ϊ����������С��Ϻ����ȡһֻ������������35![]() ��С��Ϻ������
��С��Ϻ������![]() �Ĺ���ֵ��
�Ĺ���ֵ��
��2������������С��Ϻ100ǧ�ˣ��Թ�������С��Ϻ��������
��3��Ϊ��Ӧ�г������˽�����С��Ϻ�ĿڸУ��þ����̽���40ֻС��Ϻ�ֳ������ȼ������±���
�ȼ� | һ��Ʒ | ����Ʒ | ����Ʒ |
������ |
|
|
|
���ֲ������ȡ10ֻ���������ȡ3ֻƷ������![]() Ϊ�鵽����Ʒ����������鵽����Ʒ��������
Ϊ�鵽����Ʒ����������鵽����Ʒ��������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ں���y=f��x���������䶨�����ڴ���x0 �� ʹ��x0f��x0��=1���������x0Ϊ����f��x���ġ����ȵ㡱�����к����о��С����ȵ㡱����
��f��x��=��2x+2![]() �� ��f��x��=sinx��x��[0��2��]��
�� ��f��x��=sinx��x��[0��2��]��
��f��x��=x+![]() �� x�ʣ�0��+�ޣ�����f��x��=ex�� ��f��x��=��2lnx��
�� x�ʣ�0��+�ޣ�����f��x��=ex�� ��f��x��=��2lnx��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������y=sin��2x�� ![]() ��ͼ������ƽ��
��ͼ������ƽ�� ![]() ����λ�����ú���ͼ���һ���Գ���ķ����ǣ� ��
����λ�����ú���ͼ���һ���Գ���ķ����ǣ� ��
A.x= ![]()
B.x= ![]()
C.x= ![]()
D.x=�� ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�̳����ij��Ʒ���д������������ַ�����ѡ��ÿ�ִ������������������ʵʩ����ÿ�ַ����е�һ������ڶ����µ����������.��������������ͳ�����ݣ���ʵʩ����1��Ԥ�Ƶ�һ���µ������Ǵ���ǰ��1.2����1.5���ĸ��ʷֱ���0.6��0.4���ڶ����µ������ǵ�һ���µ�1.4����1.6���ĸ��ʶ���0.5����ʵʩ����2��Ԥ�Ƶ�һ���µ������Ǵ���ǰ��1.4����1.5���ĸ��ʷֱ���0.7��0.3���ڶ����µ������ǵ�һ���µ�1.2����1.6���ĸ��ʷֱ���0.6��0.4.��![]() ��ʾʵʩ����
��ʾʵʩ����![]() �ĵڶ����µ������Ǵ���ǰ�����ı���.
�ĵڶ����µ������Ǵ���ǰ�����ı���.
������![]() ��
�� ![]() �ķֲ��У�
�ķֲ��У�
������ʵʩ���ַ����� ![]() ��ڶ����µ�����֮��Ĺ�ϵ���±����ԱȽ����ַ����ڶ����µ��������.
��ڶ����µ�����֮��Ĺ�ϵ���±����ԱȽ����ַ����ڶ����µ��������.
![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijʡ�߿��ĸ��·��������������ƣ��߿��ɼ�ʵ�С�![]() ���Ĺ���ģʽ����һ����3�������ġ���ѧ�����ÿ������150�֣��ڶ�����3���ɿ�����˼�����Ρ���ʷ����������������ѧ������6����Ŀ������ѡ������3����Ŀ�μӵȼ��Կ��ԣ�ÿ������100�֣��߿�¼ȡ�ɼ������ܷ�����750��.Ϊ�˵���ѧ������������ѧ�������ѡ�����������ij��ijһ��ѧ������������ѧ������������Ŀ������ѡ��һ�Ƶ�ѧ��������ѧ��Ⱥ��
���Ĺ���ģʽ����һ����3�������ġ���ѧ�����ÿ������150�֣��ڶ�����3���ɿ�����˼�����Ρ���ʷ����������������ѧ������6����Ŀ������ѡ������3����Ŀ�μӵȼ��Կ��ԣ�ÿ������100�֣��߿�¼ȡ�ɼ������ܷ�����750��.Ϊ�˵���ѧ������������ѧ�������ѡ�����������ij��ijһ��ѧ������������ѧ������������Ŀ������ѡ��һ�Ƶ�ѧ��������ѧ��Ⱥ��![]() ����ѧ��Ⱥ��
����ѧ��Ⱥ��![]() �������ȡ��50��ѧ�����е��飬����ѡ����������ѧ������Ŀ�Ŀ��������ͳ�����±���
�������ȡ��50��ѧ�����е��飬����ѡ����������ѧ������Ŀ�Ŀ��������ͳ�����±���

(I)���������50��ѧ������ѡ2����������ѡ����������ѧ�������Ŀ��������ȵĸ��ʣ�
(II)���������50��ѧ������ѡ2������![]() ��ʾ��2��ѧ��ѡ����������ѧ������Ŀ�Ŀ����֮��ľ���ֵ�����������
��ʾ��2��ѧ��ѡ����������ѧ������Ŀ�Ŀ����֮��ľ���ֵ�����������![]() �ķֲ��к���ѧ������
�ķֲ��к���ѧ������
(III)��Ƶ����Ϊ���ʣ��ִ�ѧ��Ⱥ��![]() �������ȡ4��ѧ����������ǡ��ѡ����������ѧ�������е�����Ŀ��ѧ��������
�������ȡ4��ѧ����������ǡ��ѡ����������ѧ�������е�����Ŀ��ѧ��������![]() �����¼���
�����¼���![]() ���ĸ���.
���ĸ���.
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com