
分析 (1)根据向量数量积的公式进行求解即可.
(2)根据向量数量积的四则运算法则进行化简求解即可.
解答 解:(1)∵|${\left.{\overrightarrow a}\right.$|=3,|${\left.{\overrightarrow b}\right.$|=4,且$\overrightarrow a$与$\overrightarrow b$的夹角为120°,
∴$\overrightarrow a$•$\overrightarrow b$=|$\overrightarrow a$|•|$\overrightarrow b$|cos120°=3×4cos120°=12×(-$\frac{1}{2}$)=6;
(2)($\overrightarrow b$-2$\overrightarrow a$)•($\overrightarrow a$+2$\overrightarrow b$)=-2|$\overrightarrow a$|2+2|$\overrightarrow b$|2-3$\overrightarrow a$•$\overrightarrow b$=-2×9+2×16-3×(-6)=-18+32+18=32;.
点评 本题主要考查向量数量积的计算以及向量数量积的四则运算,根据相应的公式是解决本题的关键.比较基础.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | 归纳推理 | B. | 演绎推理 | C. | 类比推理 | D. | 特殊推理 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ($\overrightarrow{a}$•$\overrightarrow{b}$)•$\overrightarrow{c}$=$\overrightarrow{a}$•($\overrightarrow{b}$•$\overrightarrow{c}$) | B. | $\overrightarrow{a}$•$\overrightarrow{b}$=$\overrightarrow{a}$•$\overrightarrow{c}$,则$\overrightarrow{b}$=$\overrightarrow{c}$ | ||
| C. | |$\overrightarrow{a}$•$\overrightarrow{b}$|=|$\overrightarrow{a}$|•|$\overrightarrow{b}$| | D. | 若|$\overrightarrow{a}$+$\overrightarrow{b}$|=|$\overrightarrow{a}$-$\overrightarrow{b}$|,则$\overrightarrow{a}$•$\overrightarrow{b}$=0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
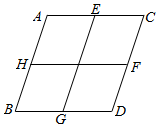 如图,在菱形ABCD中,E、F、G、H分别为四边的中点,从图形中的所有平行四边形中任取一个,取到的恰好是菱形的概率是( )
如图,在菱形ABCD中,E、F、G、H分别为四边的中点,从图形中的所有平行四边形中任取一个,取到的恰好是菱形的概率是( )| A. | $\frac{1}{2}$ | B. | $\frac{5}{8}$ | C. | $\frac{4}{9}$ | D. | $\frac{5}{9}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | 148 | B. | 126 | C. | 102 | D. | 88 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com