
【题目】已知f(x)是定义在R上的偶函数,当x≥0时,f(x)=x2﹣x
(1)求f(x)的解析式;
(2)画出f(x)的图象;
(3)若方程f(x)=k有4个解,求k的范围.
 备战中考寒假系列答案
备战中考寒假系列答案科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
, ![]() ,
, ![]() 为实数,
为实数, ![]() ,
, ![]() 为自然对数的底数,
为自然对数的底数, ![]() .
.
(1)当![]() ,
, ![]() 时,设函数
时,设函数![]() 的最小值为
的最小值为![]() ,求
,求![]() 的最大值;
的最大值;
(2)若关于![]() 的方程
的方程![]() 在区间
在区间![]() 上有两个不同实数解,求
上有两个不同实数解,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
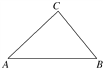
【题目】如图,在△ABC中,已知|AB|=4 ![]() ,且三内角A,B,C满足2sin A+sin C=2sin B,建立适当的坐标系,求顶点C的轨迹方程.
,且三内角A,B,C满足2sin A+sin C=2sin B,建立适当的坐标系,求顶点C的轨迹方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱柱 ![]() 中,侧面
中,侧面![]() 和侧面
和侧面![]() 都是矩形,
都是矩形, ![]() 是边长为
是边长为![]() 的正三角形,
的正三角形, ![]() 分别为
分别为![]() 的中点.
的中点.
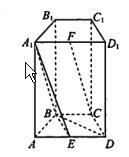
(1)求证: ![]() 平面
平面![]() ;
;
(2)求证:平面![]() 平面
平面![]() .
.
(3)若![]() 平面
平面![]() ,求棱
,求棱![]() 的长度.
的长度.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() .
.
(1)判断函数f(x)的奇偶性;
(2)判断并证明f(x)的单调性;
(3)求关于x的不等式f(2x﹣1)+f(x+3)>0的解集.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,抛物线
中,抛物线![]() 的顶点是原点,以
的顶点是原点,以![]() 轴为对称轴,且经过点
轴为对称轴,且经过点![]() .
.
(Ⅰ)求抛物线![]() 的方程;
的方程;
(Ⅱ)设点![]() ,
, ![]() 在抛物线
在抛物线![]() 上,直线
上,直线![]() ,
, ![]() 分别与
分别与![]() 轴交于点
轴交于点![]() ,
, ![]() ,
, ![]() .求直线
.求直线![]() 的斜率.
的斜率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学生在假期进行某种小商品的推销,他利用所学知识进行了市场调查,发现这种商品当天的市场价格与他的进货量(件)加上20成反比.已知这种商品每件进价为2元.他进100件这种商品时,当天卖完,利润为100元.若每天的商品都能卖完,求这个学生一天的最大利润是多少?获得最大利润时每天的进货量是多少件?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(α)= ![]() .
.
(1)若α为第二象限角且f(α)=﹣ ![]() ,求
,求 ![]() 的值;
的值;
(2)若5f(α)=4f(3α+2β).试问tan(2α+β)tan(α+β)是否为定值(其中α≠kπ+ ![]() ,α+β≠kπ+
,α+β≠kπ+ ![]() ,2α+β≠kπ+
,2α+β≠kπ+ ![]() ,3α+2β≠kπ+
,3α+2β≠kπ+ ![]() ,k∈Z)?若是,请求出定值;否则,说明理由.
,k∈Z)?若是,请求出定值;否则,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com