
【题目】(1)若动点![]() 到定点
到定点![]() 的距离与到定直线
的距离与到定直线![]() :
:![]() 的距离之比为
的距离之比为![]() ,求证:动点
,求证:动点![]() 的轨迹是椭圆;
的轨迹是椭圆;
(2)设(1)中的椭圆短轴的上顶点为![]() ,试找出一个以点
,试找出一个以点![]() 为直角顶点的等腰直角三角形
为直角顶点的等腰直角三角形![]() ,并使得
,并使得![]() 、
、![]() 两点也在椭圆上,并求出
两点也在椭圆上,并求出![]() 的面积;
的面积;
(3)对于椭圆![]() (常数
(常数![]() ),设椭圆短轴的上顶点为
),设椭圆短轴的上顶点为![]() ,试问:以点
,试问:以点![]() 为直角顶点,且
为直角顶点,且![]() 、
、![]() 两点也在椭圆上的等腰直角三角形
两点也在椭圆上的等腰直角三角形![]() 有几个?
有几个?
【答案】(1)见解析(2)![]() (3)见解析
(3)见解析
【解析】
(1)假设动点![]() 坐标,利用条件,建立等式,化简可判断动点
坐标,利用条件,建立等式,化简可判断动点![]() 的轨迹;
的轨迹;
(2)根据条件可知,![]() ,
,![]() 应是关于
应是关于![]() 轴对称,将直线方程与椭圆方程联立,从而可求
轴对称,将直线方程与椭圆方程联立,从而可求![]() 长,故可求面积;
长,故可求面积;
(3)与(2)相同的求法,将直线方程与椭圆方程联立,求![]() ,
,![]() 的长,利用
的长,利用![]() 即可得出答案.
即可得出答案.
(1)![]() 动点
动点![]() 到定点
到定点![]() 的距离与到定直线
的距离与到定直线![]() :
:![]() 的距离之比为
的距离之比为![]()
![]()
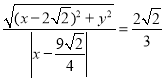 ,化简可得:
,化简可得:![]() ,
,![]() 动点
动点![]() 的轨迹是椭圆.
的轨迹是椭圆.
(2)![]() 椭圆方程为
椭圆方程为![]() ,
,![]()
又![]() 等腰直角三角形
等腰直角三角形![]() 是以
是以![]() 为直角顶点,
为直角顶点,
不妨设![]() 点在
点在![]() 轴左侧,则
轴左侧,则![]() 点在
点在![]() 轴右侧,
轴右侧,
若直线![]() 、
、![]() 关于
关于![]() 轴对称且该三角形为等腰直角三角形,可取
轴对称且该三角形为等腰直角三角形,可取![]() ,则
,则![]() ,
,
![]()
![]() ,
,![]() ,
,
联立椭圆方程和![]() 直线方程可得:
直线方程可得: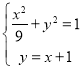 ,
,
消掉![]() :可得:
:可得:![]() ,解得
,解得![]()
![]()
![]() 故
故![]() ,可得
,可得![]()
根据两点间距离公式可得:

![]() 等腰直角三角形
等腰直角三角形![]() 是以
是以![]() 、
、![]() 为直角边,
为直角边,
![]()
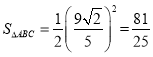 ;
;
(3)![]() 椭圆方程为
椭圆方程为![]() ,
,![]() ,设
,设![]() ,
,
联立椭圆方程和![]() 直线方程可得:
直线方程可得: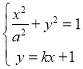 ,
,
消掉![]() 可得:
可得:![]() ,
,![]() 解得
解得![]()
![]() ,
,
又![]() 根据弦长公式可得:
根据弦长公式可得:![]() ,
,
同理可得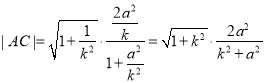 ,
,
![]()
![]() ,
,![]()
![]() ,
,
化简可得:![]() ,即:
,即:![]() ,
,
可得![]() 或
或![]()
当![]() 且
且![]() ,即
,即![]() 时,
时,![]() 有三个解,即这样的三角形有
有三个解,即这样的三角形有![]() 个;
个;
当![]() 时,即当
时,即当![]() 时,方程
时,方程![]() 为
为![]() ,解得
,解得![]() ,这样的三角形只有
,这样的三角形只有![]() 个;
个;
当![]() 时,即当
时,即当![]() 时,
时,![]() 只有一个解,即这样的三角形有
只有一个解,即这样的三角形有![]() 个.
个.


 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案科目:高中数学 来源: 题型:
【题目】已知函数![]() 的定义域是
的定义域是![]() ,且
,且![]() ,
,![]() ,当
,当![]() 时,
时,![]() .
.
(1)判断![]() 的奇偶性,并说明理由;
的奇偶性,并说明理由;
(2)求![]() 在区间
在区间![]() 上的解析式;
上的解析式;
(3)是否存在整数![]() ,使得当
,使得当![]() 时,不等式
时,不等式![]() 有解?证明你的结论.
有解?证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】过双曲线![]() 的右支上的一点P作一直线l与两渐近线交于A、B两点,其中P是
的右支上的一点P作一直线l与两渐近线交于A、B两点,其中P是![]() 的中点;
的中点;
(1)求双曲线的渐近线方程;
(2)当P坐标为![]() 时,求直线l的方程;
时,求直线l的方程;
(3)求证:![]() 是一个定值.
是一个定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若数列![]() 前
前![]() 项和为
项和为![]()
(1)若首项![]() ,且对于任意的正整数
,且对于任意的正整数![]() 均有
均有![]() ,(其中
,(其中![]() 为正实常数),试求出数列
为正实常数),试求出数列![]() 的通项公式.
的通项公式.
(2)若数列![]() 是等比数列,公比为
是等比数列,公比为![]() ,首项为
,首项为![]() ,
,![]() 为给定的正实数,满足:①
为给定的正实数,满足:①![]() ,且
,且![]() ②对任意的正整数
②对任意的正整数![]() ,均有
,均有![]() ;试求函数
;试求函数![]() 的最大值(用
的最大值(用![]() 和
和![]() 表示)
表示)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() 为实数,函数
为实数,函数![]() .
.
(1)若函数![]() 是偶函数,求实数
是偶函数,求实数![]() 的值;
的值;
(2)若![]() ,求函数
,求函数![]() 的最小值;
的最小值;
(3)对于函数![]() ,在定义域内给定区间
,在定义域内给定区间![]() ,如果存在
,如果存在![]() ,满足
,满足![]() ,则称函数
,则称函数![]() 是区间
是区间![]() 上的“平均值函数”,
上的“平均值函数”,![]() 是它的一个“均值点”.如函数
是它的一个“均值点”.如函数![]() 是
是![]() 上的平均值函数,
上的平均值函数,![]() 就是它的均值点.现有函数
就是它的均值点.现有函数![]() 是区间
是区间![]() 上的平均值函数,求实数
上的平均值函数,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的离心率
的离心率![]() ,若椭圆的左、右焦点分别为
,若椭圆的左、右焦点分别为![]() ,
,![]() ,椭圆上一动点
,椭圆上一动点![]() 和
和![]() ,
,![]() 组成
组成![]() 的面积最大为
的面积最大为![]() .
.
(1)求椭圆的方程;
(2)若存在直线![]() :
:![]() 和椭圆相交于不同的两点
和椭圆相交于不同的两点![]() ,
,![]() ,且原点
,且原点![]() 与
与![]() ,
,![]() 连线的斜率之和满足:
连线的斜率之和满足:![]() .求直线
.求直线![]() 的斜率
的斜率![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|x﹣a|+|x+1|(a∈R),g(x)=|2x﹣1|+2.
(1)若a=1,证明:不等式f(x)≤g(x)对任意的x∈R成立;
(2)若对任意的m∈R,都有t∈R,使得f(m)=g(t)成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】冬季历来是交通事故多发期,面临着货运高危运行、恶劣天气频发、包车客运监管漏洞和农村交通繁忙等四个方面的挑战.全国公安交管部门要认清形势、正视问题,针对近期事故暴露出来的问题,强薄羽、补短板、堵漏洞,进一步推动五大行动,巩固扩大五大行动成果,全力确保冬季交通安全形势稳定.据此,某网站推出了关于交通道路安全情况的调查,通过调查年龄在![]() 的人群,数据表明,交通道路安全仍是百姓最为关心的热点,参与调查者中关注此类问题的约占80%.现从参与调查并关注交通道路安全的人群中随机选出100人,并将这100人按年龄分组:第1组
的人群,数据表明,交通道路安全仍是百姓最为关心的热点,参与调查者中关注此类问题的约占80%.现从参与调查并关注交通道路安全的人群中随机选出100人,并将这100人按年龄分组:第1组![]() ,第2组
,第2组![]() ,第3组
,第3组![]() ,第4组
,第4组![]() ,第5组
,第5组![]() ,得到的频率分布直方图如图所示.
,得到的频率分布直方图如图所示.
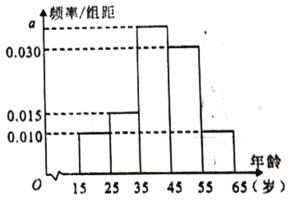
(1)求这100人年龄的样本平均数(同一组数据用该区间的中点值作代表)和中位数(精确到小数点后一位);
(2)现在要从年龄较大的第1,2组中用分层抽样的方法抽取5人,再从这5人中随机抽取2人进行问卷调查,求第2组恰好抽到1人的概率;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com