练习册

  • 练习册
  • 试题
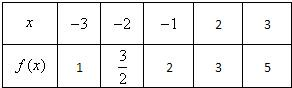
    精英家教网 > 高中数学 > 题目详情
    已知函数f(x)=满足f(1)=1,f(2)=.

    (1)求f(x)的表达式;

    (2)判断F(x)= lg［f(x)］在x∈［-1，1］上的单调性，并用定义给出证明;

    (3)若m∈R，求F(|m- |-|m+|)的值域.

    解析：（1）由已知

    （2）由（1）知

    设-1≤x1＜x2≤1,

    ?

    因为x12+1＞0,x22+1＞0,x1-x2＜0,x1x2-1＜0,所以f(x1) -f(x2)＞0,即f(x)在［-1，1］上单调递减.又?||≤||=1,?

    所以f(x)＞0, lg［f(x)］有意义.?

    所以F(x)=lg［f(x)］在［-1，1］上单调递减.??

    （3）||m-|-|m+||≤|m--(m+)|= ,

    所以-≤|m-|-|m+|≤.

    所以F()≤F(|m-|-|m+|)≤F(-).?

    而F()=lg,F(-)=lg,?

    所以所求值域为［lg,lg］.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    已知函数f（x）为R上的连续函数且存在反函数f-1（x），若函数f（x）满足下表：
    精英家教网
    那么，不等式|f-1（x-1）|＜2的解集是（　　）
    A、{x|
    5
    2
    ＜x＜4}
    B、{x|
    3
    2
    ＜x＜3}
    C、{x|1＜x＜2}
    D、{x|1＜x＜5}

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知函数f（x）=
    x+
    1
    2
    ，(x≤
    1
    2
    )
    2x-1，(
    1
    2
    ＜x＜1)
    x-1，(x≥1)
    ，若数列{an}满a1=
    7
    3
    ，an+1=f（an），n∈N*，则a2006+a2009+a2010=
     
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （2013•潍坊一模）已知函数f(x)=
    		3
    sin
    ωx+φ
    2
    cos
    ωx+φ
    2
    +sin2
    ωx+φ
    2
    (ω＞0，0＜φ＜
    π
    2
    )    ．其图象的两个相邻对称中心的距离为
    π
    2
    ，且过点(
    π
    3
    ，1)    ．
    （I）函数f（x）的达式；
    （Ⅱ）在△ABC中．a、b、c分别是角A、B、C的对边，a=
    		5
    ，S△ABC=2
    		5
    ，角C为锐角．且满f(
    C
    2
    -
    π
    12
    )=
    7
    6
    ，求c的值．

    查看答案和解析>>

    科目：高中数学 来源：聊城一中数列测试题 题型：044

    已知函数f(x)＝(x≠－1)．设数列{an}满足a1＝1，an+1＝f(an)，数列{bn}满bn＝|an－|，Sn＝b1＋b2＋…＋bn(n∈N*)

    (Ⅰ)用数学归纳法证明；

    (Ⅱ)证明．

    查看答案和解析>>

    科目：高中数学 来源：潍坊一模 题型：解答题

    已知函数f(x)=
    		3
    sin
    ωx+φ
    2
    cos
    ωx+φ
    2
    +sin2
    ωx+φ
    2
    (ω＞0，0＜φ＜
    π
    2
    )    ．其图象的两个相邻对称中心的距离为
    π
    2
    ，且过点(
    π
    3
    ，1)    ．
    （I）函数f（x）的达式；
    （Ⅱ）在△ABC中．a、b、c分别是角A、B、C的对边，a=
    		5
    ，S△ABC=2
    		5
    ，角C为锐角．且满f(
    C
    2
    -
    π
    12
    )=
    7
    6
    ，求c的值．

    查看答案和解析>>

    同步练习册答案