
【题目】(1)![]() 取何值时,方程
取何值时,方程![]() (
(![]() )无解?有一解?有两解?有三解?
)无解?有一解?有两解?有三解?
(2)函数的性质通常指函数的定义域、值域、周期性、单调性、奇偶性等,请选择适当的探究顺序,研究函数![]() 的性质,并在此基础上,作出其在
的性质,并在此基础上,作出其在![]() 的草图;
的草图;
【答案】(1)![]() 时,无解;
时,无解;![]() 时,有一解;
时,有一解;![]() 时,有两解;
时,有两解;![]() 时,有三解;
时,有三解;
(2)定义域为![]() ,值域为
,值域为![]() ,周期为
,周期为![]() ,在
,在![]() 为增函数,在
为增函数,在![]() 上为减函数,偶函数;作图见解析
上为减函数,偶函数;作图见解析
【解析】
(1)令函数![]() ,由
,由![]() ,得
,得![]() 的单调性和值域,由此得
的单调性和值域,由此得![]() 的何值范围;
的何值范围;
(2)先研究![]() 的定义域、奇偶性、周期性,再研究函数的单调性、值域,最后画出图形.
的定义域、奇偶性、周期性,再研究函数的单调性、值域,最后画出图形.
(1)令![]() ,
,![]()
![]() ,
,![]() ,
,
![]()
![]() 在
在![]() ,
,![]() 递增,在
递增,在![]() 递减,
递减,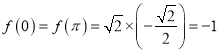 ,
,
![]() ,
,![]() ,
,
综上:![]() 时,无解;
时,无解;![]() 时,有一解;
时,有一解;![]() 时,有两解;
时,有两解;![]() 时,有三解.
时,有三解.
(2)∵![]() ,∴f(x)的定义域为R;
,∴f(x)的定义域为R;
∵![]() ,∴f(x)为偶函数;
,∴f(x)为偶函数;
∵f(x+π)=![]() =
=![]() +
+![]() =f(x),∴f(x)是周期为π的周期函数;
=f(x),∴f(x)是周期为π的周期函数;
当![]() 时,f(x)=
时,f(x)=![]() ,
,
∴当![]() 时,f(x)单调递减;当
时,f(x)单调递减;当![]() 时,
时,
f(x)=![]() ,
,
f(x)单调递增;又∵f(x)是周期为π的偶函数,
∴f(x)在![]() 上单调递增,在
上单调递增,在![]() 上单调递减(k∈Z);
上单调递减(k∈Z);
∵当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() .∴f(x)的值域为
.∴f(x)的值域为![]() ;
;
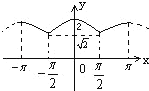
由以上性质可得:f(x)在[﹣π,π]上的图象如图所示:


科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 为正方形,
为正方形,![]() 底面
底面![]() ,
,![]() ,
,![]() 为线段
为线段![]() 的中点,若
的中点,若![]() 为线段
为线段![]() 上的动点(不含
上的动点(不含![]() ).
).
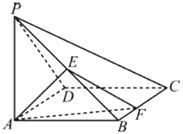
(1)平面![]() 与平面
与平面![]() 是否互相垂直?如果是,请证明;如果不是,请说明理由;
是否互相垂直?如果是,请证明;如果不是,请说明理由;
(2)求二面角![]() 的余弦值的取值范围.
的余弦值的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】关于函数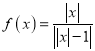 ,给出以下四个命题:(1)当
,给出以下四个命题:(1)当![]() 时,
时,![]() 单调递减且没有最值;(2)方程
单调递减且没有最值;(2)方程![]() 一定有实数解;(3)如果方程
一定有实数解;(3)如果方程![]() (
(![]() 为常数)有解,则解得个数一定是偶数;(4)
为常数)有解,则解得个数一定是偶数;(4)![]() 是偶函数且有最小值.其中假命题的序号是____________.
是偶函数且有最小值.其中假命题的序号是____________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知全集为![]() ,
,![]() ,定义集合
,定义集合![]() 的特征函数为
的特征函数为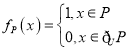 ,对于
,对于![]() ,
,![]() ,给出下列四个结论:
,给出下列四个结论:
(1)对任意![]() ,有
,有![]()
(2)对任意![]() ,若
,若![]() ,则
,则![]()
(3)对任意![]() ,有
,有![]()
(4)对任意![]() ,有
,有![]()
其中,正确的序号是_____
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某游戏棋盘上标有第![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 站,棋子开始位于第
站,棋子开始位于第![]() 站,选手抛掷均匀硬币进行游戏,若掷出正面,棋子向前跳出一站;若掷出反面,棋子向前跳出两站,直到跳到第
站,选手抛掷均匀硬币进行游戏,若掷出正面,棋子向前跳出一站;若掷出反面,棋子向前跳出两站,直到跳到第![]() 站或第
站或第![]() 站时,游戏结束.设游戏过程中棋子出现在第
站时,游戏结束.设游戏过程中棋子出现在第![]() 站的概率为
站的概率为![]() .
.
(1)当游戏开始时,若抛掷均匀硬币![]() 次后,求棋子所走站数之和
次后,求棋子所走站数之和![]() 的分布列与数学期望;
的分布列与数学期望;
(2)证明:![]() ;
;
(3)若最终棋子落在第![]() 站,则记选手落败,若最终棋子落在第
站,则记选手落败,若最终棋子落在第![]() 站,则记选手获胜.请分析这个游戏是否公平.
站,则记选手获胜.请分析这个游戏是否公平.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 的前
的前![]() 项和为
项和为![]() ,且
,且![]()
(![]() )求数列
)求数列![]() 的通项公式;
的通项公式;
(![]() )若数列
)若数列![]() 满足
满足![]() ,求数列
,求数列![]() 的通项公式;
的通项公式;
(![]() )在(
)在(![]() )的条件下,设
)的条件下,设![]() ,问是否存在实数
,问是否存在实数![]() 使得数列
使得数列![]() 是单调递增数列?若存在,求出
是单调递增数列?若存在,求出![]() 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】关于函数的对称性有如下结论:对于给定的函数![]() ,如果对于任意的
,如果对于任意的![]() 都有
都有![]() 成立
成立![]() 为常数),则函数
为常数),则函数![]() 关于点
关于点![]() 对称.
对称.
(1)用题设中的结论证明:函数![]() 关于点
关于点![]() ;
;
(2)若函数![]() 既关于点
既关于点![]() 对称,又关于点
对称,又关于点![]() 对称,且当
对称,且当![]() 时,
时,![]() ,求:①
,求:①![]() 的值;
的值;
②当![]() 时,
时,![]() 的表达式.
的表达式.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数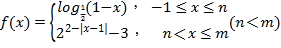 的值域是
的值域是![]() ,有下列结论:①当
,有下列结论:①当![]() 时,
时,![]() ; ②当
; ②当![]() 时,
时,![]() ;③当
;③当![]() 时,
时,![]() ; ④当
; ④当![]() 时,
时,![]() .其中结论正确的所有的序号是( ).
.其中结论正确的所有的序号是( ).
A.①②B.③④C.②③D.②④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在边长为![]() 的等边三角形
的等边三角形![]() 中,点
中,点![]() 分别是边
分别是边![]() 上的点,满足
上的点,满足![]() 且
且![]()
![]() ,将
,将![]() 沿直线
沿直线![]() 折到
折到![]() 的位置. 在翻折过程中,下列结论成立的是( )
的位置. 在翻折过程中,下列结论成立的是( )
A.在边![]() 上存在点
上存在点![]() ,使得在翻折过程中,满足
,使得在翻折过程中,满足![]() 平面
平面![]()
B.存在![]() ,使得在翻折过程中的某个位置,满足平面
,使得在翻折过程中的某个位置,满足平面![]() 平面
平面![]()
C.若![]() ,当二面角
,当二面角![]() 为直二面角时,
为直二面角时,![]()
D.在翻折过程中,四棱锥![]() 体积的最大值记为
体积的最大值记为![]() ,
,![]() 的最大值为
的最大值为![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com