【题目】如图，正方体
的棱长为1，E，F分别为棱
，AB上的点，下列说法正确的是________.（填上所有正确命题的序号）
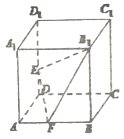
①
平面
②在平面
内总存在与平面平行的直线
③
在侧面
上的正投影是面积为定值的三角形
④当E，F为中点时，平面截该正方体所得的截面图形是五边形
【答案】②③④
【解析】
根据正方体的性质对每个命题进行判断．①根据线面垂直的性质定理判断，②根据线面平行的判定定理判断，③作出投影后可求解，④作出截面可得．
①若
平面
，则有
，
又正方体中
平面
，
在平面内，因此有
，
与
是相交直线，由有
平面
，因此有
，但只有
与
重合时，这个垂直才成立．故①错误；
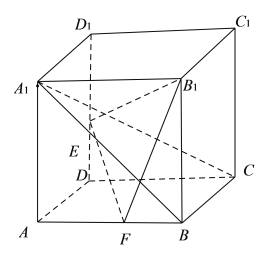
②如果任意两个平面平行，则一个平面内任一直线与另一平面平行，如果两个平面相交，则其中一个平面内与交线平行的直线必与另一平面平行．所以对任意两个平面，一个平面内一定有直线与另一平面平行，②正确；
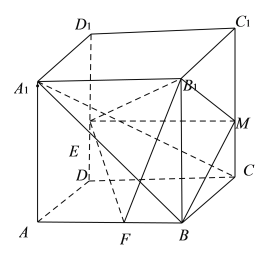
③如图，
的投影是
，的投影是
，即
的投影是
，在
上，因此的面积是定值．③正确；
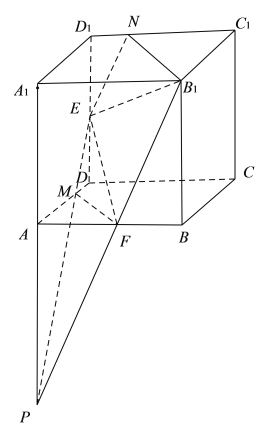
④作出完整的截面：
延长
交于点
，连接
交
于，在
上取点
，使得
．连接
，可以证明
，即在边
上，截面
是五边形，④正确．
故答案为：②③④．
新课标快乐提优暑假作业陕西旅游出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案科目：高中数学 来源： 题型：
【题目】自2017年2月底,90多所自主招生试点高校将陆续出台2017年自主招生简章,某校高三年级选取了在期中考试中成绩优异的100名学生作为调查对象,对是否准备参加2017年的自主招生考试进行了问卷调查,其中“准备参加”“不准备参加”和“待定”的人数如表:
准备参加 | 不准备参加 | 待定 | |
男生 | 30 | 6 | 15 |
女生 | 15 | 9 | 25 |
(1)在所有参加调查的同学中,在三种类型中用分层抽样的方法抽取20人进行座谈交流,则在“准备参加”“不准备参加”和“待定”的同学中应各抽取多少人?
(2)在“准备参加”的同学中用分层抽样方法抽取6人,从这6人中任意抽取2人,求至少有一名女生的概率.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】设函数y＝f（x）的定义域为R，并且满足f（x+y）＝f（x）+f（y），f（
）＝1，当x＞0时，f（x）＞0．
（1）求f（0）的值；
（2）判断函数的奇偶性；
（3）如果f（x）+f（2+x）＜2，求x的取值范围．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某商店经营的消费品进价每件14元，月销售量
（百件）与销售价格p（元）的关系如下图，每月各种开支2000元.
(1)写出月销售量（百件）与销售价格p（元）的函数关系；
(2)写出月利润y（元）与销售价格p（元）的函数关系：
(3)当商品价格每件为多少元时，月利润最大？并求出最大值.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某地区某农产品近几年的产量统计如表：
年份 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 |
年份代码t | 1 | 2 | 3 | 4 | 5 | 6 |
年产量y(万吨) | 6.6 | 6.7 | 7 | 7.1 | 7.2 | 7.4 |
（Ⅰ）根据表中数据，建立
关于的线性回归方程
；
（Ⅱ）根据线性回归方程预测2019年该地区该农产品的年产量.
附:对于一组数据
，其回归直线的斜率和截距的最小二乘估计分别为：
，
.(参考数据:
，计算结果保留小数点后两位）
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，四棱锥P-ABCD中，底面ABCD为矩形，PA⊥平面ABCD，E为PD的中点．
(1) 证明：PB∥平面AEC
(2) 设二面角D-AE-C为60°，AP=1，AD=
，求三棱锥E-ACD的体积
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知某摸球游戏的规则如下：从装有5个大小、形状完全相同的小球的盒中摸球（其中3个红球、2个黄球），每次摸一个球记录颜色并放回，若摸出红球记1分，摸出黄球记2分．
（1）求“摸球三次得分为5分”的概率；
（2）设ξ为摸球三次所得的分数，求随机变量ξ的分布列和数学期望．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
