
分析 由数量积的坐标运算求得tanα=2.
(1)展开两角和的正切,代入tanα的值得答案;
(2)把分母中的1换为sin2α+cos2α,然后分子分母同时除以cos2α,转化为正切求解.
解答 解:∵$\vec a$=(cosα,-1),$\vec b$=(2,sinα),且$\vec a•\vec b=0$,
∴2cosα-sinα=0,即tanα=2.
(1)tan(α+$\frac{π}{4}$)=$\frac{tanα+tan\frac{π}{4}}{1-tanα•tan\frac{π}{4}}=\frac{2+1}{1-2×1}=-3$;
(2)$\frac{sin2α}{{{{sin}^2}α-cos2α-1}}$=$\frac{2sinα•cosα}{si{n}^{2}α-co{s}^{2}α+si{n}^{2}α-si{n}^{2}α-co{s}^{2}α}$
=$\frac{2sinα•cosα}{si{n}^{2}α-2co{s}^{2}α}=\frac{2tanα}{ta{n}^{2}α-2}=\frac{2×2}{{2}^{2}-2}=2$.
点评 本题考查平面向量数量积的运算,考查同角三角函数基本关系式的应用,是基础题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | (-2,-1,4) | B. | (-2,1,-4) | C. | (2,1,-4) | D. | (2,-1,-4) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| x | 2 | 3 | 4 | 5 | 6 |
| y | 2 | 3 | 5 | 7 | 8 |
| A. | 1.6 | B. | 2.6 | C. | 3.6 | D. | 4.6 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
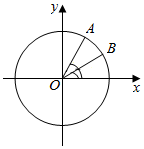 如图,在平面直角坐标系xOy中,以Ox轴为始边做锐角α和钝角β,它们的终边分别与单位圆相交于A、B两点,已知A、B的纵坐标分别为$\frac{{\sqrt{5}}}{5}$,$\frac{{\sqrt{10}}}{10}$.
如图,在平面直角坐标系xOy中,以Ox轴为始边做锐角α和钝角β,它们的终边分别与单位圆相交于A、B两点,已知A、B的纵坐标分别为$\frac{{\sqrt{5}}}{5}$,$\frac{{\sqrt{10}}}{10}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{69}{56}$ | B. | $\frac{7}{8}$ | C. | $\frac{69}{28}$ | D. | $\frac{7}{16}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 91.5和91.5 | B. | 91.5和92 | C. | 91和91.5 | D. | 92和92 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,AB为半圆O的直径,AD⊥AB,过D作圆的另一切线DC交AB的延长线于E,C为切点,连接BC,OD.
如图,AB为半圆O的直径,AD⊥AB,过D作圆的另一切线DC交AB的延长线于E,C为切点,连接BC,OD.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 分组 | [70,80) | [80,90) | [90,100) | [100,110) |
| 频数 | 3 | 4 | 8 | 15 |
| 分组 | [110,120) | [120,130) | [130,140) | [140,150] |
| 频数 | 15 | x | 3 | 2 |
| 分组 | [70,80) | [80,90) | [90,100) | [100,110) |
| 频数 | 1 | 2 | 8 | 9 |
| 分组 | [110,120) | [120,130) | [130,140) | [140,150] |
| 频数 | 10 | 10 | y | 3 |
| P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.010 |
| k0 | 2.072 | 2.706 | 3.841 | 6.635 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com