
【题目】设函数f(x)=2x3+3ax2+3bx+8c在x=1及x=2时取得极值. (Ⅰ)求a、b的值;
(Ⅱ)若对任意的x∈[0,3],都有f(x)<c2成立,求c的取值范围.
【答案】解:(Ⅰ)f'(x)=6x2+6ax+3b, 因为函数f(x)在x=1及x=2取得极值,则有f'(1)=0,f'(2)=0.
即 ![]()
解得a=﹣3,b=4.
(Ⅱ)由(Ⅰ)可知,f(x)=2x3﹣9x2+12x+8c,f'(x)=6x2﹣18x+12=6(x﹣1)(x﹣2).
当x∈(0,1)时,f'(x)>0;
当x∈(1,2)时,f'(x)<0;
当x∈(2,3)时,f'(x)>0.
所以,当x=1时,f(x)取得极大值f(1)=5+8c,又f(0)=8c,f(3)=9+8c.
则当x∈[0,3]时,f(x)的最大值为f(3)=9+8c.
因为对于任意的x∈[0,3],有f(x)<c2恒成立,
所以9+8c<c2 ,
解得c<﹣1或c>9,
因此c的取值范围为(﹣∞,﹣1)∪(9,+∞).
【解析】(1)依题意有,f'(1)=0,f'(2)=0.求解即可.(2)若对任意的x∈[0,3],都有f(x)<c2成立f(x)max<c2在区间[0,3]上成立,根据导数求出函数在[0,3]上的最大值,进一步求c的取值范围.
【考点精析】通过灵活运用函数的极值与导数和函数的最大(小)值与导数,掌握求函数![]() 的极值的方法是:(1)如果在
的极值的方法是:(1)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极大值(2)如果在
是极大值(2)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极小值;求函数
是极小值;求函数![]() 在
在![]() 上的最大值与最小值的步骤:(1)求函数
上的最大值与最小值的步骤:(1)求函数![]() 在
在![]() 内的极值;(2)将函数
内的极值;(2)将函数![]() 的各极值与端点处的函数值
的各极值与端点处的函数值![]() ,
,![]() 比较,其中最大的是一个最大值,最小的是最小值即可以解答此题.
比较,其中最大的是一个最大值,最小的是最小值即可以解答此题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】某仓库为了保持库内的湿度和温度,四周墙上均装有如图所示的自动通风设施.该设施的下部ABCD是矩形,其中AB=2米,BC=0.5米.上部CmD是个半圆,固定点E为CD的中点.△EMN是由电脑控制其形状变化的三角通风窗(阴影部分均不通风),MN是可以沿设施边框上下滑动且始终保持和AB平行的伸缩横杆(MN和AB、DC不重合). 
(1)当MN和AB之间的距离为1米时,求此时三角通风窗EMN的通风面积;
(2)设MN与AB之间的距离为x米,试将三角通风窗EMN的通风面积S(平方米)表示成关于x的函数S=f(x);
(3)当MN与AB之间的距离为多少米时,三角通风窗EMN的通风面积最大?并求出这个最大面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数F(x)= ![]() t(t﹣4)dt在[﹣1,5]上( )
t(t﹣4)dt在[﹣1,5]上( )
A.有最大值0,无最小值
B.有最大值0,最小值 ![]()
C.有最小值 ![]() ,无最大值
,无最大值
D.既无最大值也无最小值
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某仓库为了保持库内的湿度和温度,四周墙上均装有如图所示的自动通风设施.该设施的下部ABCD是矩形,其中AB=2米,BC=0.5米.上部CmD是个半圆,固定点E为CD的中点.△EMN是由电脑控制其形状变化的三角通风窗(阴影部分均不通风),MN是可以沿设施边框上下滑动且始终保持和AB平行的伸缩横杆(MN和AB、DC不重合). 
(1)当MN和AB之间的距离为1米时,求此时三角通风窗EMN的通风面积;
(2)设MN与AB之间的距离为x米,试将三角通风窗EMN的通风面积S(平方米)表示成关于x的函数S=f(x);
(3)当MN与AB之间的距离为多少米时,三角通风窗EMN的通风面积最大?并求出这个最大面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】f(x),g(x)分别是定义在R上的奇函数和偶函数,当x<0时,f′(x)g(x)+f(x)g′(x)<0且f(﹣1)=0则不等式f(x)g(x)<0的解集为( )
A.(﹣1,0)∪(1,+∞)
B.(﹣1,0)∪(0,1)
C.(﹣∞,﹣1)∪(1,+∞)
D.(﹣∞,﹣1)∪(0,1)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将正方形ABCD沿对角线BD折成直二面角A﹣BD﹣C,有如下四个结论:
(1)AC⊥BD;
(2)△ACD是等边三角形
(3)AB与平面BCD所成的角为60°;
(4)AB与CD所成的角为60°.
则正确结论的序号为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】靖国神社是日本军国主义的象征.中国人民珍爱和平,所以要坚决反对日本军国主义. 2013年12月26日日本首相安倍晋三悍然参拜靖国神社,此举在世界各国激起舆论的批评.某报的环球舆情调查中心对中国大陆七个代表性城市的1000个普通民众展开民意调查. 某城市调查体统计结果如下表:
性别 中国政府是否 需要在钓鱼岛和其他争议 问题上持续对日强硬 | 男 | 女 |
需要 | 50 | 250 |
不需要 | 100 | 150 |
(1) 试估计这七个代表性城市的普通民众中,认为 “中国政府需要在钓鱼岛和其他争议问题上持续对日强硬” 的民众所占比例;
(2) 能否有![]() 以上的把握认为这七个代表性城市的普通民众的民意与性别有关?
以上的把握认为这七个代表性城市的普通民众的民意与性别有关?
(3) 从被调查认为“中国政府需要在钓鱼岛和其他争议问题上持续对日强硬” 的民众中,采用分层抽样的方式抽取6人做进一步的问卷调查,然后在这6人中用简单随机抽样方法抽取2人进行电视专访,记被抽到的2人中女性的人数为![]() ,求
,求![]() 的分布列.
的分布列.
附: 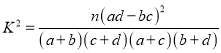
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在等比数列{an}中,an>0(n∈N*),a1a3=4,且a3+1是a2和a4的等差中项,
若bn=log2an+1.
(1)求数列{bn}的通项公式;
(2)若数列{cn}满足cn=an+1+![]() ,求数列{cn}的前n项和.
,求数列{cn}的前n项和.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com