
【题目】设函数![]() .
.
(1)讨论函数![]() 的单调性;
的单调性;
(2)若函数![]() 在
在![]() 时恒成立,求实数
时恒成立,求实数![]() 的取值范围;
的取值范围;
(3)若函数![]() ,求证:函数
,求证:函数![]() 的极大值小于1.
的极大值小于1.
【答案】(1)见解析;(2)![]() (3)见证明
(3)见证明
【解析】
(1)先对函数求导,分别讨论![]() 和
和![]() ,即可得出结果;
,即可得出结果;
(2)先将函数![]() 在
在![]() 时恒成立,转化为
时恒成立,转化为![]() 在
在![]() 上恒成立,再设
上恒成立,再设![]() ,
,![]() ,利用导数方法求出
,利用导数方法求出![]() 的最大值,即可得出结果;
的最大值,即可得出结果;
(3)先由题意得到![]() ,对
,对![]() 求导,利用导数的方法研究其单调性,即可求出其极大值,得出结论.
求导,利用导数的方法研究其单调性,即可求出其极大值,得出结论.
解:(1)由于![]() ,
,![]() ,
,
当![]() 时,
时,![]() ,
,![]() 在
在![]() 上单调递减;
上单调递减;
当![]() 时,由
时,由![]() 得
得![]() ,由
,由![]() 得
得![]() ;
;
所以![]() 在
在![]() 上单调递减,
上单调递减,![]() 上单调递增.
上单调递增.
(2)若![]() 在
在![]() 上恒成立,
上恒成立,
只需![]() ,
,![]() .
.
令![]() ,
,![]() ,则
,则![]() ,
,
由![]() 得
得![]() ,所以
,所以
![]() ,
,![]() 随
随![]() 的变化情况如下:
的变化情况如下:
|
| 1 |
|
| + | 0 | - |
|
| 极大值 |
|
所以![]() ,所以
,所以![]() .
.
(3)由题知![]() ,
,![]() ,
,
令![]() ,
,![]() ,
,
则函数![]() 在
在![]() 上单调递减,
上单调递减,![]() ,
,![]() ,
,
所以存在唯一的![]() ,
,
当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() .
.
所以函数![]() 的单调递增区间是
的单调递增区间是![]() ,单调递减区间是
,单调递减区间是![]() ,
,
其中![]() ,所以函数
,所以函数![]() 有极大值.
有极大值.
函数![]() 的极大值是
的极大值是![]() ,由
,由![]() ,得
,得![]() ,
,
所以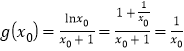 ,因为
,因为![]() ,所以
,所以![]() ,即
,即![]() ,
,
所以![]() 的极大值小于1.
的极大值小于1.


科目:高中数学 来源: 题型:
【题目】据调查显示,某高校![]() 万男生的身高服从正态分布
万男生的身高服从正态分布![]() ,现从该校男生中随机抽取
,现从该校男生中随机抽取![]() 名进行身高测量,将测量结果分成
名进行身高测量,将测量结果分成![]() 组:
组: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,并绘制成如图所示的频率分布直方图.
,并绘制成如图所示的频率分布直方图.
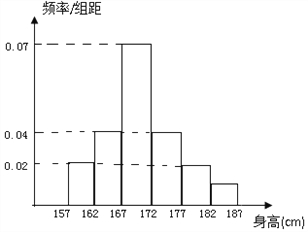
(Ⅰ)求这![]() 名男生中身高在
名男生中身高在![]() (含
(含![]() )以上的人数;
)以上的人数;
(Ⅱ)从这![]() 名男生中身高在
名男生中身高在![]() 以上(含
以上(含![]() )的人中任意抽取
)的人中任意抽取![]() 人,该
人,该![]() 人中身高排名(从高到低)在全校前
人中身高排名(从高到低)在全校前![]() 名的人数记为
名的人数记为![]() ,求
,求![]() 的数学期望.
的数学期望.
(附:参考数据:若![]() 服从正态分布
服从正态分布![]() ,则
,则![]() ,
, ![]() ,
, ![]() .)
.)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知向量![]() =(sinx,cosx),
=(sinx,cosx),![]() =(sin(x﹣
=(sin(x﹣![]() ),sinx),函数f(x)=2
),sinx),函数f(x)=2![]()
![]() ,g(x)=f(
,g(x)=f(![]() ).
).
(1)求f(x)在[![]() ,π]上的最值,并求出相应的x的值;
,π]上的最值,并求出相应的x的值;
(2)计算g(1)+g(2)+g(3)+…+g(2014)的值;
(3)已知t∈R,讨论g(x)在[t,t+2]上零点的个数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】![]() 年春节期间,某服装超市举办了一次有奖促销活动,消费每超过
年春节期间,某服装超市举办了一次有奖促销活动,消费每超过![]() 元(含
元(含![]() 元),均可抽奖一次,抽奖方案有两种,顾客只能选择其中的一种.方案一:从装有
元),均可抽奖一次,抽奖方案有两种,顾客只能选择其中的一种.方案一:从装有![]() 个形状、大小完全相同的小球(其中红球
个形状、大小完全相同的小球(其中红球![]() 个,黑球
个,黑球![]() 个)的抽奖盒中,一次性摸出
个)的抽奖盒中,一次性摸出![]() 个球,其中奖规则为:若摸到
个球,其中奖规则为:若摸到![]() 个红球,享受免单优惠;若摸出
个红球,享受免单优惠;若摸出![]() 个红球则打
个红球则打![]() 折,若摸出
折,若摸出![]() 个红球,则打
个红球,则打![]() 折;若没摸出红球,则不打折.方案二:从装有
折;若没摸出红球,则不打折.方案二:从装有![]() 个形状、大小完全相同的小球(其中红球
个形状、大小完全相同的小球(其中红球![]() 个,黑球
个,黑球![]() 个)的抽奖盒中,有放回每次摸取
个)的抽奖盒中,有放回每次摸取![]() 球,连摸
球,连摸![]() 次,每摸到
次,每摸到![]() 次红球,立减
次红球,立减![]() 元.
元.
(1)若两个顾客均分别消费了![]() 元,且均选择抽奖方案一,试求两位顾客均享受免单优惠的概率;
元,且均选择抽奖方案一,试求两位顾客均享受免单优惠的概率;
(2)若某顾客消费恰好满![]() 元,试从概率的角度比较该顾客选择哪一种抽奖方案更合算?
元,试从概率的角度比较该顾客选择哪一种抽奖方案更合算?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设直线![]() 与抛物线
与抛物线![]() 交于
交于![]() ,
,![]() 两点,与椭圆
两点,与椭圆![]() 交于
交于![]() ,
,![]() 两点,直线
两点,直线![]() ,
,![]() ,
,![]() ,
,![]() (
(![]() 为坐标原点)的斜率分别为
为坐标原点)的斜率分别为![]() ,
,![]() ,
,![]() ,
,![]() ,若
,若![]() .
.
(1)是否存在实数![]() ,满足
,满足![]() ,并说明理由;
,并说明理由;
(2)求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
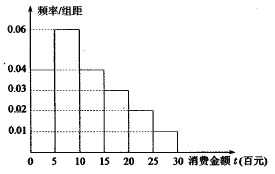
【题目】“双十一”已经成为网民们的网购狂欢节,某电子商务平台对某市的网民在今年“双十一”的网购情况进行摸底调查,用随机抽样的方法抽取了100人,其消费金额![]() (百元)的频率分布直方图如图所示:
(百元)的频率分布直方图如图所示:
(1)求网民消费金额![]() 的平均值和中位数
的平均值和中位数![]() ;
;
(2)把下表中空格里的数填上,能否有![]() 的把握认为网购消费与性别有关;
的把握认为网购消费与性别有关;
男 | 女 | 合计 | |
| |||
| 30 | ||
合计 | 45 |
附表:
|
|
|
|
|
|
|
|
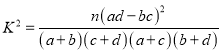 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】古代数学名著《九章算术》中的“盈不足”问题知两鼠穿垣.今有垣厚5尺,两鼠对穿.大鼠日一尺,小鼠亦一尺.大鼠日自倍,小鼠日自半.问:何日相逢?题意是:由垛厚五尺(旧制长度单位, ![]() 尺=
尺= ![]() 寸)的墙壁,大小两只老鼠同时从墙的两面,沿一直线相对打洞.大鼠第一天打进
寸)的墙壁,大小两只老鼠同时从墙的两面,沿一直线相对打洞.大鼠第一天打进![]() 尺,以后每天的速度为前一天的
尺,以后每天的速度为前一天的![]() 倍;小鼠第一天也打进
倍;小鼠第一天也打进![]() 尺,以后每天的进度是前一天的一半.它们多久可以相遇?
尺,以后每天的进度是前一天的一半.它们多久可以相遇?
A. ![]() 天 B.
天 B. ![]() 天 C.
天 C. ![]() 天 D.
天 D. ![]() 天
天
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某同学用“五点法”画函数![]() 在某一个周期内的图象时,列表并填入了部分数据,如下表:
在某一个周期内的图象时,列表并填入了部分数据,如下表:
| 0 |
|
|
|
|
|
|
| |||
| 0 | 2 | 0 | 0 |
(1)请将上表数据补充完整,填写在相应位置,并求出函数![]() 的解析式;
的解析式;
(2)把![]() 的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),再把得到的图象向左平移
的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),再把得到的图象向左平移![]() 个单位长度,得到函数
个单位长度,得到函数![]() 的图象,求
的图象,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com