
ЁОЬтФПЁПЮЊСЫбаОПЙњУёЪеШыдкЙњУёжЎМфЕФЗжХфЃЌБмУтЦЖИЛЙ§ЗжаќЪтЃЌУРЙњЭГМЦбЇМвРЭТзДФЬсГіСЫжјУћЕФРЭТзДФЧњЯпЃЌШчЭМЫљЪОЃКРЭТзДФЧњЯпЮЊжБЯп![]() ЪБЃЌБэЪОЪеШыЭъШЋЦНЕШЃЌРЭТзДФЧњЯпЮЊелЯп
ЪБЃЌБэЪОЪеШыЭъШЋЦНЕШЃЌРЭТзДФЧњЯпЮЊелЯп![]() ЪБЃЌБэЪОЪеШыЭъШЋВЛЦНЕШМЧЧјгђ
ЪБЃЌБэЪОЪеШыЭъШЋВЛЦНЕШМЧЧјгђ![]() ЮЊВЛЦНЕШЧјгђЃЌ
ЮЊВЛЦНЕШЧјгђЃЌ![]() БэЪОЦфУцЛ§ЃЌ
БэЪОЦфУцЛ§ЃЌ![]() ЮЊ
ЮЊ![]() ЕФУцЛ§ЃЎНЋ
ЕФУцЛ§ЃЎНЋ![]() ЃЌГЦЮЊЛљФсЯЕЪ§ЃЎЖдгкЯТСаЫЕЗЈЃК
ЃЌГЦЮЊЛљФсЯЕЪ§ЃЎЖдгкЯТСаЫЕЗЈЃК
Ђй![]() дНаЁЃЌдђЙњУёЗжХфдНЙЋЦНЃЛ
дНаЁЃЌдђЙњУёЗжХфдНЙЋЦНЃЛ
ЂкЩшРЭТзДФЧњЯпЖдгІЕФКЏЪ§ЮЊ![]() ЃЌдђЖд
ЃЌдђЖд![]() ЃЌОљга
ЃЌОљга![]() ЃЛ
ЃЛ
ЂлШєФГЙњМвФГФъЕФРЭТзДФЧњЯпНќЫЦЮЊ![]() ЃЌдђ
ЃЌдђ![]() ЃЛ
ЃЛ
ЂмШєФГЙњМвФГФъЕФРЭТзДФЧњЯпНќЫЦЮЊ![]() ЃЌдђ
ЃЌдђ![]() ЃЎ
ЃЎ
ЦфжаВЛе§ШЗЕФЪЧЃКЃЈ ЃЉ
A.ЂйЂмB.ЂкЂлC.ЂйЂлЂмD.ЂйЂкЂм
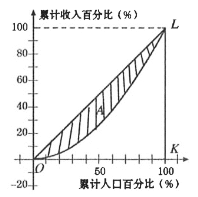
 УћаЃЬсЗжвЛОэЭЈЯЕСаД№АИ
УћаЃЬсЗжвЛОэЭЈЯЕСаД№АИ ПЮГЬДяБъВтЪдОэДГЙи100ЗжЯЕСаД№АИ
ПЮГЬДяБъВтЪдОэДГЙи100ЗжЯЕСаД№АИ аТОэЭѕЦкФЉГхДЬ100ЗжЯЕСаД№АИ
аТОэЭѕЦкФЉГхДЬ100ЗжЯЕСаД№АИ ШЋФмДГЙи100ЗжЯЕСаД№АИ
ШЋФмДГЙи100ЗжЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЭждВ![]() ЕФжааФЮЊдЕу
ЕФжааФЮЊдЕу![]() ЃЌНЙЕуЮЊ
ЃЌНЙЕуЮЊ![]() ЃЌРыаФТЪЮЊ
ЃЌРыаФТЪЮЊ![]() ЃЌВЛгызјБъжсДЙжБЕФжБЯп
ЃЌВЛгызјБъжсДЙжБЕФжБЯп![]() гыЭждВ
гыЭждВ![]() НЛгк
НЛгк![]() ЃЌ
ЃЌ![]() СНЕу.
СНЕу.
ЃЈ1ЃЉШє![]() ЮЊЯпЖЮ
ЮЊЯпЖЮ![]() ЕФжаЕуЃЌЧѓжБЯп
ЕФжаЕуЃЌЧѓжБЯп![]() ЕФЗНГЬ.
ЕФЗНГЬ.
ЃЈ2ЃЉШєЕу![]() ЪЧжБЯп
ЪЧжБЯп![]() ЩЯвЛЕуЃЌЕу
ЩЯвЛЕуЃЌЕу![]() дкЭждВ
дкЭждВ![]() ЩЯЃЌЧвТњзу
ЩЯЃЌЧвТњзу![]() ЃЌЩшжБЯп
ЃЌЩшжБЯп![]() гыжБЯп
гыжБЯп![]() ЕФаБТЪЗжБ№ЮЊ
ЕФаБТЪЗжБ№ЮЊ![]() ЃЌ
ЃЌ![]() ЃЌЮЪ
ЃЌЮЪ![]() ЪЧЗёЮЊЖЈжЕЃПШєЪЧЃЌЧыЧѓГі
ЪЧЗёЮЊЖЈжЕЃПШєЪЧЃЌЧыЧѓГі![]() ЕФжЕЃЛШєВЛЪЧЃЌЧыЫЕУїРэгЩ.
ЕФжЕЃЛШєВЛЪЧЃЌЧыЫЕУїРэгЩ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкжБНЧзјБъЯЕжа![]() жаЃЌЧњЯп
жаЃЌЧњЯп![]() ЕФВЮЪ§ЗНГЬЮЊ
ЕФВЮЪ§ЗНГЬЮЊ![]() ЃЈ
ЃЈ![]() ЮЊВЮЪ§ЃЌ
ЮЊВЮЪ§ЃЌ![]() ЃЉ.вдзјБъдЕуЮЊМЋЕуЃЌ
ЃЉ.вдзјБъдЕуЮЊМЋЕуЃЌ![]() жсе§АыжсЮЊМЋжсНЈСЂМЋзјБъЯЕЃЌвбжЊжБЯп
жсе§АыжсЮЊМЋжсНЈСЂМЋзјБъЯЕЃЌвбжЊжБЯп![]() ЕФМЋзјБъЗНГЬЮЊ
ЕФМЋзјБъЗНГЬЮЊ![]() .
.
ЃЈ1ЃЉЩш![]() ЪЧЧњЯп
ЪЧЧњЯп![]() ЩЯЕФвЛИіЖЏЕуЃЌЕБ
ЩЯЕФвЛИіЖЏЕуЃЌЕБ![]() ЪБЃЌЧѓЕу
ЪБЃЌЧѓЕу![]() ЕНжБЯп
ЕНжБЯп![]() ЕФОрРыЕФзюДѓжЕЃЛ
ЕФОрРыЕФзюДѓжЕЃЛ
ЃЈ2ЃЉШєЧњЯп![]() ЩЯЫљгаЕФЕуОљдкжБЯп
ЩЯЫљгаЕФЕуОљдкжБЯп![]() ЕФгвЯТЗНЃЌЧѓ
ЕФгвЯТЗНЃЌЧѓ![]() ЕФШЁжЕЗЖЮЇ.
ЕФШЁжЕЗЖЮЇ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊКЏЪ§![]() .
.
ЃЈЂёЃЉШєжБЯп![]() дкЕу
дкЕу![]() ДІЧаЯпЗНГЬЮЊ
ДІЧаЯпЗНГЬЮЊ![]() ЃЌЧѓЪЕЪ§
ЃЌЧѓЪЕЪ§![]() ЕФжЕЃЛ
ЕФжЕЃЛ
ЃЈЂђЃЉШєКЏЪ§![]() га3ИіСуЕуЃЌЧѓЪЕЪ§
га3ИіСуЕуЃЌЧѓЪЕЪ§![]() ЕФШЁжЕЗЖЮЇ.
ЕФШЁжЕЗЖЮЇ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊКЏЪ§![]() ЃЌ
ЃЌ![]() .
.
ЃЈ1ЃЉЬжТл![]() ЕФЕЅЕїадЃЛ
ЕФЕЅЕїадЃЛ
ЃЈ2ЃЉЖЈвхЃКЖдгкКЏЪ§![]() ЃЌШєДцдк
ЃЌШєДцдк![]() ЃЌЪЙ
ЃЌЪЙ![]() ГЩСЂЃЌдђГЦ
ГЩСЂЃЌдђГЦ![]() ЮЊКЏЪ§
ЮЊКЏЪ§![]() ЕФВЛЖЏЕу.ШчЙћКЏЪ§
ЕФВЛЖЏЕу.ШчЙћКЏЪ§![]() ДцдкВЛЖЏЕуЃЌЧѓЪЕЪ§
ДцдкВЛЖЏЕуЃЌЧѓЪЕЪ§![]() ЕФШЁжЕЗЖЮЇ.
ЕФШЁжЕЗЖЮЇ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГИпжажОдИепФажОдИеп5ШЫЃЌХЎжОдИеп3ШЫЃЌетаЉШЫвЊВЮМгЩчЧјЗўЮёЙЄзї.ДгетаЉШЫжаЫцЛњГщШЁ4ШЫИКд№ЮФУїаћДЋЙЄзїЃЌСэЭт4ШЫИКд№ЮРЩњЗўЮёЙЄзї.
ЃЈЂёЃЉЩш![]() ЮЊЪТМўЃЛЁАИКд№ЮФУїаћДЋЙЄзїЕФжОдИепжаАќКЌХЎжОдИепМзЕЋВЛАќКЌФажОдИепввЁБЃЌЧѓЪТМў
ЮЊЪТМўЃЛЁАИКд№ЮФУїаћДЋЙЄзїЕФжОдИепжаАќКЌХЎжОдИепМзЕЋВЛАќКЌФажОдИепввЁБЃЌЧѓЪТМў![]() ЗЂЩњЕФИХТЪЃЛ
ЗЂЩњЕФИХТЪЃЛ
ЃЈЂђЃЉЩш![]() БэЪОВЮМгЮФУїаћДЋЙЄзїЕФХЎжОдИепШЫЪ§ЃЌЧѓЫцЛњБфСП
БэЪОВЮМгЮФУїаћДЋЙЄзїЕФХЎжОдИепШЫЪ§ЃЌЧѓЫцЛњБфСП![]() ЕФЗжВМСагыЪ§бЇЦкЭћ.
ЕФЗжВМСагыЪ§бЇЦкЭћ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвбжЊХзЮяЯпx2ЃН2pyЃЈpЃО0ЃЉЕФНЙЕуЮЊFЃЈ0ЃЌ1ЃЉЃЌЙ§FЕФСНЬѕЖЏжБЯпABЃЌCDгыХзЮяЯпНЛГіAЁЂBЁЂCЁЂDЫФЕуЃЌжБЯпABЃЌCDЕФаБТЪДцдкЧвЗжБ№ЪЧk1ЃЈk1ЃО0ЃЉЃЌk2ЃЎ
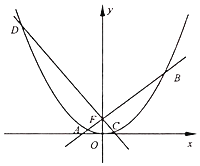
ЃЈЂёЃЉШєжБЯпBDЙ§ЕуЃЈ0ЃЌ3ЃЉЃЌЧѓжБЯпACгыyжсЕФНЛЕузјБъ
ЃЈЂђЃЉШєk1Љk2ЃН2ЃЌЧѓЫФБпаЮACBDУцЛ§ЕФзюаЁжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊКЏЪ§![]() ЃЌЪЕЪ§
ЃЌЪЕЪ§![]() .
.
ЃЈ1ЃЉЬжТлКЏЪ§![]() дкЧјМф
дкЧјМф![]() ЩЯЕФЕЅЕїадЃЛ
ЩЯЕФЕЅЕїадЃЛ
ЃЈ2ЃЉШєДцдк![]() ЃЌЪЙЕУЙигкxЕФВЛЕШЪН
ЃЌЪЙЕУЙигкxЕФВЛЕШЪН![]() ГЩСЂЃЌЧѓЪЕЪ§aЕФШЁжЕЗЖЮЇ.
ГЩСЂЃЌЧѓЪЕЪ§aЕФШЁжЕЗЖЮЇ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊжБЯпlЃК ![]() ЭждВCЃК
ЭждВCЃК ![]() ЃЌ
ЃЌ![]() ЗжБ№ЮЊЭждВЕФзѓгвНЙЕу.
ЗжБ№ЮЊЭждВЕФзѓгвНЙЕу.
ЃЈ1ЃЉЕБжБЯпlЙ§гвНЙЕу![]() ЪБЃЌЧѓCЕФБъзМЗНГЬЃЛ
ЪБЃЌЧѓCЕФБъзМЗНГЬЃЛ
ЃЈ2ЃЉЩшжБЯпlгыЭждВCНЛгкAЃЌBСНЕуЃЌOЮЊзјБъдЕуЃЌШєЁЯAOBЪЧЖлНЧЃЌЧѓЪЕЪ§aЕФШЁжЕЗЖЮЇ.
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com