
【题目】已知抛物线![]() :
:![]() 上一点
上一点![]() 到其焦点
到其焦点![]() 的距离为2.
的距离为2.
(Ⅰ)求抛物线![]() 的标准方程;
的标准方程;
(Ⅱ)设抛物线![]() 的准线与
的准线与![]() 轴交于点
轴交于点![]() ,直线
,直线![]() 过点
过点![]() 且与抛物线
且与抛物线![]() 交于
交于![]() ,
,![]() 两点(点
两点(点![]() 在点
在点![]() ,
,![]() 之间),点
之间),点![]() 满足
满足![]() ,求
,求![]() 与
与![]() 的面积之和取得最小值时直线
的面积之和取得最小值时直线![]() 的方程.
的方程.
【答案】(Ⅰ)![]() (Ⅱ)
(Ⅱ)![]() 或
或![]() .
.
【解析】
(Ⅰ)由题意知,抛物线的焦点![]() 为
为![]() ,把点
,把点![]() 代入抛物线方程,再结合点
代入抛物线方程,再结合点![]() 到其焦点
到其焦点![]() 的距离为2,利用两点间距离公式得到关于
的距离为2,利用两点间距离公式得到关于![]() 的方程,解方程即可求解;
的方程,解方程即可求解;
(Ⅱ)由(Ⅰ)知,点![]() ,易知直线
,易知直线![]() 的斜率存在,且不为零,设其方程为
的斜率存在,且不为零,设其方程为![]() ,
,
设![]() ,
,![]() ,由
,由![]() ,利用平面向量的坐标运算可得,
,利用平面向量的坐标运算可得,![]() ,联立直线方程和抛物线方程得到关于
,联立直线方程和抛物线方程得到关于![]() 的一元二次方程,利用韦达定理求出
的一元二次方程,利用韦达定理求出![]() 的值,利用数形结合可得,
的值,利用数形结合可得,![]() ,再利用基本不等式求最值即可求解.
,再利用基本不等式求最值即可求解.
(Ⅰ)![]() 的焦点为
的焦点为![]() ,依题意有
,依题意有 ,解得
,解得![]() ,
,
所以,抛物线![]() 的标准方程为
的标准方程为![]() .
.
(Ⅱ)由(Ⅰ)知,抛物线![]() 的标准方程为
的标准方程为![]() ,其准线方程为:
,其准线方程为:![]() ,
,
所以点![]() 易知直线
易知直线![]() 的斜率存在,且不为零,其方程为
的斜率存在,且不为零,其方程为![]() ,
,
设![]() ,
,![]() ,因为
,因为![]() ,即
,即![]() ,
,
∴![]() ,联立方程
,联立方程![]() ,消去
,消去![]() ,得
,得![]() ,
,![]() ,
,
根据题意,作图如下:

![]()
![]()
![]()
![]() .
.
当且仅当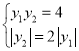 ,即
,即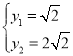 或
或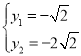 时,
时,
![]() 与
与![]() 的面积之和最小,最小值为
的面积之和最小,最小值为![]() .
.
![]() 时,
时,![]() ,
,![]() ,直线
,直线![]() 的方程为
的方程为![]() ;
;
![]() 时,
时,![]() ,
,![]() ,直线
,直线![]() 的方程为
的方程为![]() ,
,
∴![]() 与
与![]() 的面积之和最小值时直线
的面积之和最小值时直线![]() 的方程为
的方程为![]() 或
或![]() .
.


 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案科目:高中数学 来源: 题型:
【题目】近年来,随着“一带一路”倡议的推进,中国与沿线国家旅游合作越来越密切,中国到“一带一路”沿线国家的游客人也越来越多,如图是2013-2018年中国到“一带一路”沿线国家的游客人次情况,则下列说法正确的是( )
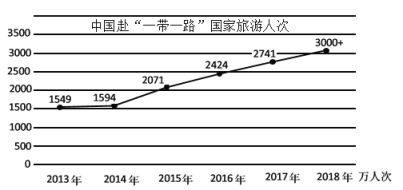
①2013-2018年中国到“一带一路”沿线国家的游客人次逐年增加
②2013-2018年这6年中,2014年中国到“一带一路”沿线国家的游客人次增幅最小
③2016-2018年这3年中,中国到“一带一路”沿线国家的游客人次每年的增幅基本持平
A.①②③B.②③C.①②D.③
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,
,![]() 为椭圆
为椭圆![]() 上任意一点,且已知
上任意一点,且已知![]() .
.
(1)若椭圆![]() 的短轴长为
的短轴长为![]() ,求
,求![]() 的最大值;
的最大值;
(2)若直线![]() 交椭圆
交椭圆![]() 的另一个点为
的另一个点为![]() ,直线
,直线![]() 交
交![]() 轴于点
轴于点![]() ,点
,点![]() 关于直线
关于直线![]() 对称点为
对称点为![]() ,且
,且![]() ,
,![]() 三点共线,求椭圆
三点共线,求椭圆![]() 的标准方程.
的标准方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知空间几何体![]() 是由圆柱切割而成的阴影部分构成,其中
是由圆柱切割而成的阴影部分构成,其中![]() ,
,![]() 为下底面圆直径的两个端点,
为下底面圆直径的两个端点,![]() ,
,![]() 为上底面圆直径的两个端点,且
为上底面圆直径的两个端点,且![]() ,圆柱底面半径是1,高是2,则空间几何体
,圆柱底面半径是1,高是2,则空间几何体![]() 可以无缝的穿过下列哪个图形( )
可以无缝的穿过下列哪个图形( )
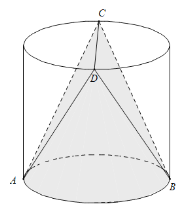
A.椭圆B.等腰直角三角形C.正三角形D.正方形
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设抛物线![]() 的焦点为
的焦点为![]() ,直线
,直线![]() 与抛物线交于
与抛物线交于![]() 两点.
两点.
(1)若![]() 过点
过点![]() ,且
,且![]() ,求
,求![]() 的斜率;
的斜率;
(2)若![]() ,且
,且![]() 的斜率为
的斜率为![]() ,当
,当![]() 时,求
时,求![]() 在
在![]() 轴上的截距的取值范围(用
轴上的截距的取值范围(用![]() 表示),并证明
表示),并证明![]() 的平分线始终与
的平分线始终与![]() 轴平行.
轴平行.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2020年1月10日,引发新冠肺炎疫情的COVID-9病毒基因序列公布后,科学家们便开始了病毒疫苗的研究过程.但是类似这种病毒疫苗的研制需要科学的流程,不是一朝一夕能完成的,其中有一步就是做动物试验.已知一个科研团队用小白鼠做接种试验,检测接种疫苗后是否出现抗体.试验设计是:每天接种一次,3天为一个接种周期.已知小白鼠接种后当天出现抗体的概率为![]() ,假设每次接种后当天是否出现抗体与上次接种无关.
,假设每次接种后当天是否出现抗体与上次接种无关.
(1)求一个接种周期内出现抗体次数![]() 的分布列;
的分布列;
(2)已知每天接种一次花费100元,现有以下两种试验方案:
①若在一个接种周期内连续2次出现抗体即终止本周期试验,进行下一接种周期,试验持续三个接种周期,设此种试验方式的花费为![]() 元;
元;
②若在一个接种周期内出现2次或3次抗体,该周期结束后终止试验,已知试验至多持续三个接种周期,设此种试验方式的花费为![]() 元.
元.
比较随机变量![]() 和
和![]() 的数学期望的大小.
的数学期望的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司以客户满意为出发点,随机抽选2000名客户,以调查问卷的形式分析影响客户满意度的各项因素.每名客户填写一个因素,下图为客户满意度分析的帕累托图.帕累托图用双直角坐标系表示,左边纵坐标表示频数,右边纵坐标表示频率,分析线表示累计频率,横坐标表示影响满意度的各项因素,按影响程度(即频数)的大小从左到右排列,以下结论正确的个数是( ).
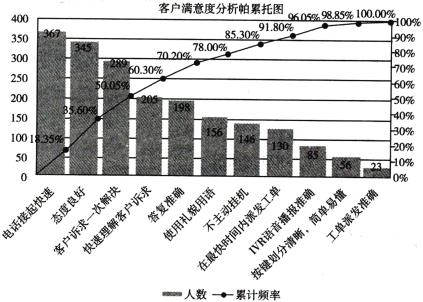
①35.6%的客户认为态度良好影响他们的满意度;
②156位客户认为使用礼貌用语影响他们的满意度;
③最影响客户满意度的因素是电话接起快速;
④不超过10%的客户认为工单派发准确影响他们的满意度.
A.1B.2C.3D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,以椭圆的2个焦点与1个短轴端点为顶点的三角形的面积为2
,以椭圆的2个焦点与1个短轴端点为顶点的三角形的面积为2![]() 。
。
(1)求椭圆的方程;
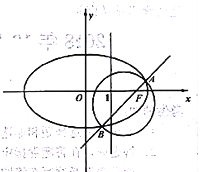
(2)如图,斜率为k的直线l过椭圆的右焦点F,且与椭圆交与A,B两点,以线段AB为直径的圆截直线x=1所得的弦的长度为![]() ,求直线l的方程。
,求直线l的方程。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知三棱锥![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() .有以下结论:①三棱锥
.有以下结论:①三棱锥![]() 的表面积为
的表面积为![]() ;②三棱锥
;②三棱锥![]() 的内切球的半径
的内切球的半径![]() ;③点
;③点![]() 到平面
到平面![]() 的距离为
的距离为![]() ;其中正确的是( )
;其中正确的是( )
A.①②B.②③C.①③D.①②③
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com