
【题目】已知函数 ![]() 在
在 ![]() 处有极值
处有极值 ![]() .
.
(1)求 ![]() ,
, ![]() 的值;
的值;
(2)判断函数 ![]() 的单调性并求出单调区间.
的单调性并求出单调区间.
【答案】
(1)解:f′(x)=2ax+ ![]() ,
,
又f(x)在x=1处有极值 ![]() ,
,
∴ 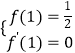 ,即
,即 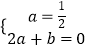
解得a= ![]() ,b=-1.
,b=-1.
经检验得a= ![]() ,b=-1函数f(x)=ax2+blnx在x=1处有极值
,b=-1函数f(x)=ax2+blnx在x=1处有极值 ![]() .
.
(2)解:由(1)可知f(x)= ![]() x2-lnx,其定义域是(0,+∞),且f′(x)=x-
x2-lnx,其定义域是(0,+∞),且f′(x)=x- ![]() =
= ![]() .
.
令f′(x)=0,解得x=1或x=-1(舍去).
当x变化时,f′(x),f(x)的变化情况如下表:
x | (0,1) | 1 | (1,+∞) |
f′(x) | - | 0 | + |
f(x) | 极小值 |
所以函数y=f(x)的单调减区间是(0,1),单调增区间是(1,+∞).
【解析】(1)根据题意求出导函数利用极值的定义列出关于a和b的函数式即可求出结果。(2)利用导函数以及极值的情况求出函数的单调性。


科目:高中数学 来源: 题型:
【题目】随着国家二孩政策的全面放开,为了调查一线城市和非一线城市的二孩生育意愿,某机构用简单随机抽样方法从不同地区调查了100位育龄妇女,结果如表.
非一线 | 一线 | 总计 | |
愿生 | 45 | 20 | 65 |
不愿生 | 13 | 22 | 35 |
总计 | 58 | 42 | 100 |
附表:
P(K2≥k) | 0.050 | 0.010 | 0.001 |
k | 3.841 | 6.635 | 10.828 |
由K2= ![]() 算得,K2=
算得,K2= ![]() ≈9.616参照附表,得到的正确结论是( )
≈9.616参照附表,得到的正确结论是( )
A.在犯错误的概率不超过0.1%的前提下,认为“生育意愿与城市级别有关”
B.在犯错误的概率不超过0.1%的前提下,认为“生育意愿与城市级别无关”
C.有99%以上的把握认为“生育意愿与城市级别有关”
D.有99%以上的把握认为“生育意愿与城市级别无关”
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法错误的是( )
A.命题“若 ![]() ,则
,则 ![]() ”的逆否命题为:“若
”的逆否命题为:“若 ![]() ,则
,则 ![]() ”
”
B.“ ![]() ”是“
”是“ ![]() ”的充分不必要条件
”的充分不必要条件
C.若 ![]() 且
且 ![]() 为假命题,则
为假命题,则 ![]() 、
、 ![]() 均为假命题
均为假命题
D.命题 ![]() :“
:“ ![]() ,使得
,使得 ![]() ”,则
”,则 ![]() :“
:“ ![]() ,均有
,均有 ![]() ”
”
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题正确的个数为( )
①“x∈R都有x2≥0”的否定是“x0∈R使得x02≤0”;
②“x≠3”是“|x|≠3”成立的充分条件;
③命题“若m≤ ![]() ,则方程mx2+2x+2=0有实数根”的否命题为真命题.
,则方程mx2+2x+2=0有实数根”的否命题为真命题.
A.0
B.1
C.2
D.3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设双曲线 ![]() (a>0,b>0)的左焦点为F1 , 左顶点为A,过F1作x轴的垂线交双曲线于P、Q两点,过P作PM垂直QA于M,过Q作QN垂直PA于N,设PM与QN的交点为B,若B到直线PQ的距离大于a+
(a>0,b>0)的左焦点为F1 , 左顶点为A,过F1作x轴的垂线交双曲线于P、Q两点,过P作PM垂直QA于M,过Q作QN垂直PA于N,设PM与QN的交点为B,若B到直线PQ的距离大于a+ ![]() ,则该双曲线的离心率取值范围是( )
,则该双曲线的离心率取值范围是( )
A.(1﹣ ![]() )
)
B.( ![]() ,+∞)
,+∞)
C.(1,2 ![]() )
)
D.(2 ![]() ,+∞)
,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两地相距![]() ,汽车从甲地行驶到乙地,速度不得超过
,汽车从甲地行驶到乙地,速度不得超过![]() ,已知汽车每小时的运输成本(以元为单位)由可变部分和固定部分组成:可变部分与速度
,已知汽车每小时的运输成本(以元为单位)由可变部分和固定部分组成:可变部分与速度![]() (
(![]() )的平方成正比,比例系数为
)的平方成正比,比例系数为![]() ,固定部分为
,固定部分为![]() 元,
元,
(1)把全程运输成本![]() (元)表示为速度
(元)表示为速度![]() (
(![]() )的函数,指出定义域;
)的函数,指出定义域;
(2)为了使全程运输成本最小,汽车应以多大速度行驶?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com