
分析 (1)求出导函数,f′(x)=ex+x+$\frac{1}{x+m}$,利用切线方程,列出方程组,求解m,n,即可顶点函数的解析式.
(2)利用f(x)≥$\frac{{x}^{2}}{2}$+ax+3对于?x>0恒成立,转化ex+ln(x+m)-ax-2≥0对于?x>0恒成立,令F(x)=ex+ln(x+e)-ax-2,通过函数的导数,二次导数,判断函数的单调性,求解函数的最小值,1)当a$≤1+\frac{1}{e}$时,2)当$a>1+\frac{1}{e}$时,F'(0)<0,方便判断求解即可.
解答 解:(1)由题意知f′(x)=ex+x+$\frac{1}{x+m}$,$\left\{{\begin{array}{l}{f(0)=3}\\{f'(0)=\frac{e+1}{e}}\end{array}}\right.$,
即$\left\{\begin{array}{l}{1+lnm+n=3}\\{1+\frac{1}{m}=\frac{e+1}{e}}\end{array}\right.$,所以$\left\{\begin{array}{l}{m=e}\\{n=1}\end{array}\right.$.
函数f(x)=ex+$\frac{{x}^{2}}{2}$+ln(x+e)+1; (4分)
(2)f(x)≥$\frac{{x}^{2}}{2}$+ax+3对于?x>0恒成立,
即ex+ln(x+m)-ax-2≥0对于?x>0恒成立,
令F(x)=ex+ln(x+e)-ax-2,F′(x)=ex+$\frac{1}{x+e}$-a,$F''(x)={e^x}-\frac{1}{{{{(x+e)}^2}}}$,
当x>0时ex≥1,$\frac{1}{{{{(x+e)}^2}}}≤1$,
所以F′′(x)>0对于?x≥0恒成立,所以F'(x)在[0,+∞)单调递增 (6分)${F'_{min}}(x)=F'(0)=1+\frac{1}{e}-a$,
1)当$1+\frac{1}{e}-a≥0$,即a$≤1+\frac{1}{e}$时,F′(x)≥0且尽在x=0时等号成立,
所以F(x)在[0,+∞)单调递增,从而F(x)≥F(0)=0,满足题意,(8分)
2)当$1+\frac{1}{e}-a<0$即$a>1+\frac{1}{e}$时,F'(0)<0,
$F'(lna)={e^{lna}}+\frac{1}{e+lna}-a=\frac{1}{e+lna}>0$且F'(x)在[0,+∞)单调递增,
所以?x0∈(0,lna),使得F′(x)=0,(10分)
当x∈(0,x0)时,F′(x)<0,所以F(x)在(0,x0)单调递减,
当x∈(x0,+∞)时,F'(x)>0,所以F(x)在(x0,+∞)单调递增,
因此,当x∈(0,x0)时,F(x)<F(0)=0,不合题意.
综上所述:$a≤1+\frac{1}{e}$(12分)
点评 本题考查函数的导数的综合应用,函数的解析式以及函数的最值的求法,考查转化思想以及计算能力.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ①② | B. | ②③ | C. | ③④ | D. | ②④ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ?x∈R,x3>x | B. | ?x∈R,x3<x | C. | ?x∈R,x3≤x | D. | ?x0∈R,x03≤x0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
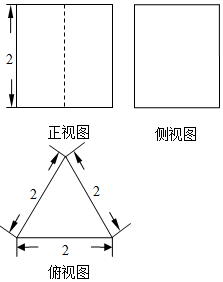 如图所示,是一个空间几何体的三视图,且这个空间几何体的所有顶点都在同一个球面上,则这个球的体积是( )
如图所示,是一个空间几何体的三视图,且这个空间几何体的所有顶点都在同一个球面上,则这个球的体积是( )| A. | $\frac{49}{9}π$ | B. | $\frac{{28\sqrt{21}}}{27}π$ | C. | $\frac{28}{3}π$ | D. | $\frac{{28\sqrt{7}}}{9}π$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com