设{an}是正数组成的数列,其前n项和为Sn,且对于所有的正整数n,有4Sn=(an+1)2.
(I)求a1,a2的值;
(II)求数列{an}的通项公式;
(III)令b1=1,b2k=a2k-1+(-1)k,b2k+1=a2k+3k(k=1,2,3,…),求{bn}的前20项和T20.
解:(I)当n=1时,4a
1=(a
1+1)
2
∴(a
1-1)
2=0,a
1=1
当n=2时,4(a
1+a
2)=(a
2+1)
2,
∴a
2=3.(3分)
(II)∵4S
n=(a
n+1)
2,4S
n-1=(a
n-1+1)
2,相减得:(a
n+a
n-1)(a
n-a
n-1-2)=0
∵{a
n}是正数组成的数列
∴a
n-a
n-1=2,∴a
n=2n-1.(8分)
(Ⅲ)T
20=b
1+[a
1+(-1)
1]+(a
2+3
1)+[a
3+(-1)
2]+(a
4+3
2)+…+[a
19+(-1)
10]
=1+S
19+(3+3
2+…+3
9)=
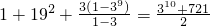
.(14分)
分析:(I)求a
1,a
2的值,对n赋值即可算得;
(II)求数列{a
n}的通项公式,需对题目中条件4S
n=(a
n+1)
2,对任意非负正整数恒成立进行理解,并依据其形式来构造出4S
n-1=(a
n-1+1)
2,作差整理出a
n-a
n-1=2判断出数列是等差数列来.
(III)的求解应根据题设中的条件将前20项的和T
20.表示出来,然后再根据具体的形式来求解.
点评:本题是一个层层推进式的题,其中第II问构造出另一个恒等式是难点,III的求解需根据具体形式来分组分别求解.

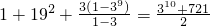 .(14分)
.(14分)
