
°æƒø°ø∆Ù∂´ –’˛∏ƃ‚‘⁄µ˚∫˛Ω®“ª∏ˆ¬√”Œπ€π‚œÓƒø,…˺∆∑Ω∞∏»Áœ¬£∫»ÁÕºÀ˘ 浃‘≤O «‘≤–Œ∫˛µƒ±þΩÁ,—ÿœþ∂ŒAB,BC,CD,DAΩ®“ª∏ˆπ€æ∞≥§¿»,∆‰÷–A,B,C,D «π€æ∞≥§¿»µƒÀƒ∏ˆ≥ˆ»Îø⁄«“∂º‘⁄‘≤O…œ£¨“—÷™£∫BC=12∞Ÿ√◊,AB=8∞Ÿ√◊,‘⁄∫˛÷–P¥¶∫Õ∫˛±þD¥¶∏˜Ω®“ª∏ˆπ€æ∞Õ§,«“À¸√«πÿ”⁄÷±œþAC∂‘≥∆,‘⁄∫˛√ÊΩ®“ªÃıπ€æ∞«≈APC.π€æ∞Õ§µƒ¥Û–°°¢π€æ∞≥§¿»°¢π€æ∞«≈µƒøÌ∂»æ˘∫ˆ¬‘≤ªº∆£¨…Ë![]() £Æ
£Æ
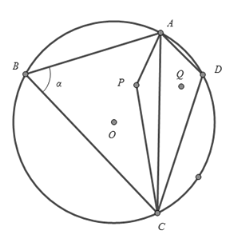
£®1£©»Ùπ€æ∞≥§¿»AD£Ω4∞Ÿ√◊£¨CD=AB£¨«Û”…π€æ∞≥§¿»À˘Œß≥…µƒÀƒ±þ–ŒABCDƒ⁄µƒ∫˛√Ê√ʪ˝£ª
£®2£©µ±![]() ±£¨«Û»˝Ω«–Œ«¯”ÚADCƒ⁄µƒ∫˛√Ê√ʪ˝µƒ◊Ó¥Û÷µ£ª
±£¨«Û»˝Ω«–Œ«¯”ÚADCƒ⁄µƒ∫˛√Ê√ʪ˝µƒ◊Ó¥Û÷µ£ª
£®3£©»ÙCD=8∞Ÿ√◊«“πʪÆΩ®Õ§µ„P‘⁄»˝Ω«–ŒABC«¯”Úƒ⁄£®≤ª∞¸¿®±þΩÁ£©£¨ ‘≈–∂œÀƒ±þ–ŒABCPƒ⁄∫˛√Ê√ʪ˝ «∑Ò”–◊Ó¥Û÷µ£ø»Ù”–£¨«Û≥ˆ◊Ó¥Û÷µ£¨≤¢–¥≥ˆ¥À ±![]() µƒ÷µ£ª»Ù√ª”–£¨«ÎÀµ√˜¿Ì”…£Æ
µƒ÷µ£ª»Ù√ª”–£¨«ÎÀµ√˜¿Ì”…£Æ
°æ¥∞∏°ø£®1£©![]() ∆Ω∑Ω∞Ÿ√◊£ª£®2£©
∆Ω∑Ω∞Ÿ√◊£ª£®2£©![]() ∆Ω∑Ω∞Ÿ√◊£ª£®3£©µ±
∆Ω∑Ω∞Ÿ√◊£ª£®3£©µ±![]() =
=![]() ±£¨Àƒ±þ–ŒABCPƒ⁄µƒ∫˛√Ê√ʪ˝»°µΩ◊Ó¥Û÷µ£¨ ◊Ó¥Û÷µŒ™32∆Ω∑Ω∞Ÿ√◊.
±£¨Àƒ±þ–ŒABCPƒ⁄µƒ∫˛√Ê√ʪ˝»°µΩ◊Ó¥Û÷µ£¨ ◊Ó¥Û÷µŒ™32∆Ω∑Ω∞Ÿ√◊.
°æΩ‚Œˆ°ø
£®1£©∑÷±‘⁄![]() ∫Õ
∫Õ![]() ÷–‘À”√”ýœ“∂®¿Ì£¨«Û≥ˆ
÷–‘À”√”ýœ“∂®¿Ì£¨«Û≥ˆ![]() £¨Ω¯∂¯ø…µ√
£¨Ω¯∂¯ø…µ√![]() ∫Õ
∫Õ![]() £¨∏˘æð
£¨∏˘æð![]() º¥ø…µ√Ω·π˚£ª£®2£©‘⁄
º¥ø…µ√Ω·π˚£ª£®2£©‘⁄![]() ÷–£¨ø…µ√
÷–£¨ø…µ√![]() £¨¡Ó
£¨¡Ó![]() £¨
£¨![]() £¨‘⁄
£¨‘⁄![]() ÷–£¨‘À”√”ýœ“∂®¿Ìø…µ√
÷–£¨‘À”√”ýœ“∂®¿Ìø…µ√![]() £¨”…ª˘±æ≤ªµ» Ωø…µ√
£¨”…ª˘±æ≤ªµ» Ωø…µ√![]() £¨”…
£¨”…![]() º¥ø…µ√Ω·π˚£ª£®3£©œ»«Û≥ˆ
º¥ø…µ√Ω·π˚£ª£®3£©œ»«Û≥ˆ![]() £¨º∆À„≥ˆ
£¨º∆À„≥ˆ![]() £¨Ω¯∂¯ø…µ√Ω·π˚.
£¨Ω¯∂¯ø…µ√Ω·π˚.
Ω‚£∫£®1£©°þÀƒ±þ–ŒABCDƒ⁄Ω””⁄‘≤O£¨°ý![]() ABC+
ABC+![]() ADC=
ADC=![]()
‘⁄![]() ÷–£¨
÷–£¨![]()
‘⁄![]() ÷–£¨
÷–£¨![]()
Ω‚µ√![]() £¨°ý
£¨°ý![]()
°ý![]()
£®∆Ω∑Ω∞Ÿ√◊£©
¥£∫Àƒ±þ–ŒABCDƒ⁄µƒ∫˛√Ê√ʪ˝ «![]() ∆Ω∑Ω∞Ÿ√◊.
∆Ω∑Ω∞Ÿ√◊.
£®2£©°þ![]() =60
=60![]() £¨°ý‘⁄
£¨°ý‘⁄![]() ÷–£¨
÷–£¨![]() =112
=112
¡Ó![]() £¨
£¨![]() £¨ ‘⁄
£¨ ‘⁄![]() ÷–£¨
÷–£¨![]() =112
=112
°ý![]() =112
=112
°þ![]()
°ý![]() £®µ±«“Ωˆµ±x=y ±£¨»°µ»∫≈£©
£®µ±«“Ωˆµ±x=y ±£¨»°µ»∫≈£©
°þ![]()
°ý![]() £®∆Ω∑Ω∞Ÿ√◊£©
£®∆Ω∑Ω∞Ÿ√◊£©
¥£∫»˝Ω«–Œ«¯”ÚADCƒ⁄µƒ∫˛√Ê√ʪ˝◊Ó¥Û÷µ![]() ∆Ω∑Ω∞Ÿ√◊£Æ
∆Ω∑Ω∞Ÿ√◊£Æ
£®3£©°þµ„P∫Õµ„Dπÿ”⁄÷±œþAC∂‘≥∆£¨
°ý![]() APC=
APC=![]() ADC£¨PC=CD=8
ADC£¨PC=CD=8
”…£®1£©÷™![]() ABC+
ABC+![]() ADC=
ADC=![]() £¨°ý
£¨°ý![]() ABC+
ABC+![]() APC=
APC=![]()
°þ![]() ABC=
ABC=![]() £¨°ý
£¨°ý![]() APC=
APC=![]()
![]()
°þµ„P‘⁄![]() «¯”Úƒ⁄
«¯”Úƒ⁄
°ý![]() £¨°ý
£¨°ý![]()
°þ‘⁄![]() ÷–£¨
÷–£¨![]()
‘⁄![]() ÷–£¨
÷–£¨![]()
°ý![]()
Ω‚µ√![]() ªÚ
ªÚ![]() £®…·»•£©
£®…·»•£©
![]()
![]()
°þ![]() £¨°ýÀƒ±þ–ŒABCPƒ⁄µƒ∫˛√Ê√ʪ˝”–◊Ó¥Û÷µ£¨
£¨°ýÀƒ±þ–ŒABCPƒ⁄µƒ∫˛√Ê√ʪ˝”–◊Ó¥Û÷µ£¨
¥£∫µ±![]() =
=![]() ±£¨Àƒ±þ–ŒABCPƒ⁄µƒ∫˛√Ê√ʪ˝»°µΩ◊Ó¥Û÷µ£¨◊Ó¥Û÷µŒ™32∆Ω∑Ω∞Ÿ√◊
±£¨Àƒ±þ–ŒABCPƒ⁄µƒ∫˛√Ê√ʪ˝»°µΩ◊Ó¥Û÷µ£¨◊Ó¥Û÷µŒ™32∆Ω∑Ω∞Ÿ√◊


 «ß¿Ô¬Ì◊þœÚºŸ∆⁄∆⁄ƒ©∑¬’Ê ‘æÌ∫ƺŸœµ¡–¥∞∏
«ß¿Ô¬Ì◊þœÚºŸ∆⁄∆⁄ƒ©∑¬’Ê ‘æÌ∫ƺŸœµ¡–¥∞∏
| ƒÍº∂ | ∏þ÷–øŒ≥à | ƒÍº∂ | ≥ı÷–øŒ≥à |
| ∏þ“ª | ∏þ“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı“ª | ≥ı“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ∂˛ | ∏þ∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı∂˛ | ≥ı∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ»˝ | ∏þ»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı»˝ | ≥ı»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° |
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø“—÷™ ˝¡–1£¨1£¨2£¨1£¨2£¨4£¨1£¨2£¨4£¨8£¨1£¨2£¨4£¨8£¨16£¨°≠£¨∆‰÷–µ⁄“ªœÓ «![]() £¨Ω”œ¬¿¥µƒ¡ΩœÓ «
£¨Ω”œ¬¿¥µƒ¡ΩœÓ «![]() £¨
£¨![]() £¨‘ŸΩ”œ¬¿¥µƒ»˝œÓ «
£¨‘ŸΩ”œ¬¿¥µƒ»˝œÓ «![]() £¨
£¨![]() £¨
£¨![]() £¨“¿¥À¿ýÕ∆£¨»Ù∏√ ˝¡–«∞
£¨“¿¥À¿ýÕ∆£¨»Ù∏√ ˝¡–«∞![]() œÓ∫Õ
œÓ∫Õ![]() ¬˙◊„£∫¢Ÿ
¬˙◊„£∫¢Ÿ![]() ¢⁄
¢⁄![]() «2µƒ’˚ ˝¥Œ√𣨑ڬ˙◊„Ãıº˛µƒ◊Ó–°µƒ
«2µƒ’˚ ˝¥Œ√𣨑ڬ˙◊„Ãıº˛µƒ◊Ó–°µƒ![]() Œ™
Ϊ
A. 21B. 91C. 95D. 10
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø Æ∂˛…˙–§£¨”÷≥∆ Æ∂˛ Ùœý£¨÷–π˙π≈»Àƒ√ Æ∂˛÷÷∂،Կ¥≈‰ Æ∂˛µÿ÷ߣ¨◊È≥…◊” Û°¢≥Û≈£°¢“˙ª¢°¢√ÆÕ√°¢≥Ω¡˙°¢À»…þ°¢ŒÁ¬Ì°¢Œ¥—Ú°¢…Í∫Ô°¢”œº¶°¢–Áπ∑°¢∫•÷Ì Æ∂˛ Ùœý°£œ÷”– Æ∂˛…˙–§º™œÈŒÔ∏˜“ªº˛£¨º◊°¢““°¢±˚»˝ŒªÕ¨—ß“ª¥ŒÀʪ˙≥È»°“ªº˛◊˜Œ™¿ÒŒÔ£¨º◊Õ¨—ßœ≤ª∂¬Ì°¢≈££¨““Õ¨—ßœ≤ª∂¬Ì°¢¡˙°¢π∑£¨±˚Õ¨—ß≥˝¡À Û≤ªœ≤ª∂Õ‚∆‰À˚µƒ∂ºœ≤ª∂£¨‘Ú’‚»˝ŒªÕ¨—ß≥È»°µƒ¿ÒŒÔ∂ºœ≤ª∂µƒ∏≈¬ «( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø‘⁄∆Ω√Ê÷±Ω«◊¯±Íœµ![]() ÷–£¨π˝∂®µ„
÷–£¨π˝∂®µ„![]() ◊˜÷±œþ”Î≈◊ŒÔœþ
◊˜÷±œþ”Î≈◊ŒÔœþ![]() œýΩª”⁄
œýΩª”⁄![]() °¢
°¢![]() ¡Ωµ„£Æ
¡Ωµ„£Æ
£®1£©“—÷™![]() £¨»Ùµ„
£¨»Ùµ„![]() «µ„
«µ„![]() πÿ”⁄◊¯±Í‘≠µ„
πÿ”⁄◊¯±Í‘≠µ„![]() µƒ∂‘≥∆µ„£¨«Û
µƒ∂‘≥∆µ„£¨«Û![]() √ʪ˝µƒ◊Ó–°÷µ£ª
√ʪ˝µƒ◊Ó–°÷µ£ª
£®2£© «∑ҥʑ⁄¥π÷±”⁄![]() ÷·µƒ÷±œþ
÷·µƒ÷±œþ![]() £¨ πµ√
£¨ πµ√![]() ±ª“‘
±ª“‘![]() Œ™÷±æ∂µƒ‘≤Ωÿµ√µƒœ“≥§∫„Œ™∂®÷µ£ø»Ù¥Ê‘⁄£¨«Û≥ˆ
Œ™÷±æ∂µƒ‘≤Ωÿµ√µƒœ“≥§∫„Œ™∂®÷µ£ø»Ù¥Ê‘⁄£¨«Û≥ˆ![]() µƒ∑Ω≥㪻Ù≤ª¥Ê‘⁄£¨Àµ√˜¿Ì”…£Æ
µƒ∑Ω≥㪻Ù≤ª¥Ê‘⁄£¨Àµ√˜¿Ì”…£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø“—÷™∫Ø ˝![]()
£®¢Ò£©»Ù![]() £¨«Û«˙œþ
£¨«Û«˙œþ![]() ‘⁄µ„
‘⁄µ„![]() ¥¶µƒ«–œþ∑Ω≥ãª
¥¶µƒ«–œþ∑Ω≥ãª
£®¢Ú£©»Ù![]() ‘⁄
‘⁄![]() …œ∫„≥…¡¢£¨«Û µ ˝
…œ∫„≥…¡¢£¨«Û µ ˝![]() µƒ»°÷µ∑∂Œß£ª
µƒ»°÷µ∑∂Œß£ª
£®¢Û£©»Ù ˝¡–![]() µƒ«∞
µƒ«∞![]() œÓ∫Õ
œÓ∫Õ![]() £¨
£¨ ![]() £¨«Û÷§£∫ ˝¡–
£¨«Û÷§£∫ ˝¡–![]() µƒ«∞
µƒ«∞![]() œÓ∫Õ
œÓ∫Õ![]() .
.
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø…Ë ˝¡–![]() µƒ«∞
µƒ«∞![]() œÓ∫ÕŒ™
œÓ∫ÕŒ™![]() £¨“—÷™
£¨“—÷™![]() .
.
£®1£©«Û ˝¡–![]() µƒÕ®œÓπ´ Ω£ª
µƒÕ®œÓπ´ Ω£ª
£®2£©»Ù∂‘»Œ“‚µƒ![]() £¨≤ªµ» Ω
£¨≤ªµ» Ω![]() ∫„≥…¡¢£¨«Û µ ˝
∫„≥…¡¢£¨«Û µ ˝![]() µƒ»°÷µ∑∂Œß.
µƒ»°÷µ∑∂Œß.
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø“—÷™∏˜œÓæ˘Œ™’˝’˚ ˝µƒ ˝¡–{an}µƒ«∞nœÓ∫ÕŒ™Sn£¨¬˙◊„£∫Sn©Å1+kan£Ωtan2©Å1£¨n°ð2£¨n° N*£®∆‰÷–k£¨tŒ™≥£ ˝£©£Æ
£®1£©»Ùk£Ω![]() £¨t£Ω
£¨t£Ω![]() £¨ ˝¡–{an} «µ»≤Ó ˝¡–£¨«Ûa1µƒ÷µ£ª
£¨ ˝¡–{an} «µ»≤Ó ˝¡–£¨«Ûa1µƒ÷µ£ª
£®2£©»Ù ˝¡–{an} «µ»±» ˝¡–£¨«Û÷§£∫k£ºt£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø“—÷™’˝œÓ ˝¡–![]() µƒ«∞
µƒ«∞![]() œÓ∫ÕŒ™
œÓ∫ÕŒ™![]() £¨«“
£¨«“![]() £¨
£¨![]() £¨ ˝¡–
£¨ ˝¡–![]() ¬˙◊„
¬˙◊„![]() £¨«“
£¨«“![]()
£®I£©«Û ˝¡–![]() £¨
£¨![]() µƒÕ®œÓπ´ Ω£ª
µƒÕ®œÓπ´ Ω£ª
£®II£©¡Ó![]() £¨«Û ˝¡–
£¨«Û ˝¡–![]() µƒ«∞
µƒ«∞![]() œÓ∫Õ
œÓ∫Õ![]() °£
°£
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø2019ƒÍ£¨∫”±±µ»8 °π´≤º¡À∏þøº∏ƒ∏Ô◊€∫œ∑Ω∞∏Ω´≤…»°°∞![]() °±ƒ£ Ω£¨º¥”ÔŒƒ°¢ ˝—ß°¢”¢”Ô±ÿøº£¨»ª∫Ûøº…˙œ»‘⁄ŒÔ¿Ì°¢¿˙ ∑÷–—°‘Ò1√≈£¨‘Ÿ‘⁄ÀºœÎ’˛÷Œ°¢µÿ¿Ì°¢ªØ—ß°¢…˙ŒÔ÷–—°‘Ò2√≈.Œ™¡À∏¸∫√Ω¯––…˙—ƒπʪƣ¨’≈√˜Õ¨—ß∂‘∏þ“ª“ªƒÍ¿¥µƒ∆þ¥Œøº ‘≥…º®Ω¯––Õ≥º∆∑÷Œˆ£¨∆‰÷–ŒÔ¿Ì°¢¿˙ ∑≥…º®µƒæ•“∂Õº»ÁÕºÀ˘ æ.
°±ƒ£ Ω£¨º¥”ÔŒƒ°¢ ˝—ß°¢”¢”Ô±ÿøº£¨»ª∫Ûøº…˙œ»‘⁄ŒÔ¿Ì°¢¿˙ ∑÷–—°‘Ò1√≈£¨‘Ÿ‘⁄ÀºœÎ’˛÷Œ°¢µÿ¿Ì°¢ªØ—ß°¢…˙ŒÔ÷–—°‘Ò2√≈.Œ™¡À∏¸∫√Ω¯––…˙—ƒπʪƣ¨’≈√˜Õ¨—ß∂‘∏þ“ª“ªƒÍ¿¥µƒ∆þ¥Œøº ‘≥…º®Ω¯––Õ≥º∆∑÷Œˆ£¨∆‰÷–ŒÔ¿Ì°¢¿˙ ∑≥…º®µƒæ•“∂Õº»ÁÕºÀ˘ æ.
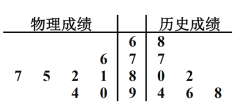
£®1£©»Ù’≈√˜Õ¨—ßÀʪ˙—°‘Ò3√≈π¶øŒ£¨«ÛÀ˚—°µΩŒÔ¿Ì’˛÷Œ¡Ω√≈π¶øŒµƒ∏≈¬ £ª
£®2£© ‘∏˘æðæ•“∂Õº∑÷Œˆ’≈√˜Õ¨—ß”¶‘⁄ŒÔ¿Ì∫Õ¿˙ ∑÷–—°‘Òƒƒ∏ˆ—ßø∆£ø≤¢≤˚ ˆ¿Ì”….
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
∞Ÿ∂»÷¬–≈ - ¡∑œ∞≤·¡–±Ì - ‘¡–±Ì
∫˛±± °ª•¡™Õ¯Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®∆Ωî | Õ¯…œ”–∫¶–≈œ¢æŸ±®◊®«¯ | µÁ–≈’©∆≠柱®◊®«¯ | …Ê¿˙ ∑–ÈŒÞ÷˜“”–∫¶–≈œ¢æŸ±®◊®«¯ | …Ê∆Û«÷»®æŸ±®◊®«¯
Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®µÁª∞£∫027-86699610 柱®” œ‰£∫58377363@163.com