
分析 欲求所投的点落在阴影部分内部的概率,须结合定积分计算阴影部分平面区域的面积,再根据几何概型概率计算公式易求解.
解答  解:曲线x2+y2=|x|+|y|所围成的区域为分别以($\frac{1}{2}$,$\frac{1}{2}$),(-$\frac{1}{2}$,$\frac{1}{2}$),(-$\frac{1}{2}$,-$\frac{1}{2}$),($\frac{1}{2}$,-$\frac{1}{2}$),为圆心,以$\frac{\sqrt{2}}{2}$为半径的圆,如图所示的面积,其面积为4×π×$\frac{1}{2}$-2($\frac{π}{2}$-1)=π+2,
解:曲线x2+y2=|x|+|y|所围成的区域为分别以($\frac{1}{2}$,$\frac{1}{2}$),(-$\frac{1}{2}$,$\frac{1}{2}$),(-$\frac{1}{2}$,-$\frac{1}{2}$),($\frac{1}{2}$,-$\frac{1}{2}$),为圆心,以$\frac{\sqrt{2}}{2}$为半径的圆,如图所示的面积,其面积为4×π×$\frac{1}{2}$-2($\frac{π}{2}$-1)=π+2,
y=1-x2与x轴所围成区域S=${∫}_{-1}^{1}$(1-x2)dx=(x-$\frac{1}{3}$x3)|${\;}_{-1}^{1}$=$\frac{4}{3}$,
故这点正好落在y=1-x2与x轴所围成区域内的概率为$\frac{4}{3π+6}$,
故答案为:$\frac{4}{3π+6}$.
点评 本题考查几何概型的计算,涉及定积分在求面积中的应用,关键是正确计算出阴影部分的面积.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
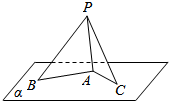 如图所示,8m高旗杆PA直立在地面α上,拉绳PB与地面α成30°的角,拉绳PC在地面α上的射影AC的长是8m.求:
如图所示,8m高旗杆PA直立在地面α上,拉绳PB与地面α成30°的角,拉绳PC在地面α上的射影AC的长是8m.求:查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{4}{3}$ | B. | $\frac{3}{4}$ | C. | -$\frac{4}{3}$ | D. | -$\frac{3}{4}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com