
函数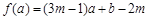 ,当
,当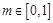 时,
时,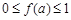 恒成立,则
恒成立,则 的最大值与最小值之和为( )
的最大值与最小值之和为( )
| A.18 | B.16 | C.14 | D.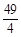 |
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:单选题
某企业生产甲、乙两种产品,已知生产每吨甲产品要用A原料3吨、B原料2吨;生产每吨乙产品要用A原料1吨、B原料3吨.销售每吨甲产品可获得利润5万元、每吨乙产品可获得利润3万元,该企业在一个生产周期内消耗A原料不超过13吨、B原料不超过18吨,那么该企业可获得的最大利润是( )
| A.12万元 | B.20万元 | C.25万元 | D.27万元 |
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
已知O是坐标原点,点A(-1,1),若点M(x,y)为平面区域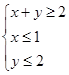 ,上的一个动点,则
,上的一个动点,则 ·
·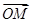 的取值范围是( )
的取值范围是( )
| A.[-1,0] | B.[0,1] | C.[0,2] | D.[-1,2] |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com