设
是首项为正数的等比数列，公比为
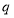，则“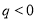
” 是“对任意的正整数
” 的_________条件. （填“充要条件、充分不必要条件、必要不充分条件、即不充分也不必要条件” ）
科目：高中数学 来源：2017届江苏泰州中学高三理上学期月考一数学试卷（解析版） 题型：解答题
设函数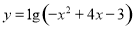
的定义域为
，函数
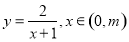的值域为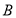
．
（1）当
时，求
；
（2）若“
”是“
”的必要不充分条件，求实数
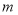的取值范围．
查看答案和解析>>
科目：高中数学 来源：2017届江苏泰州中学高三上学期期中数学试卷（解析版） 题型：解答题
设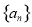
是公差为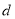
的等差数列，
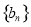是公比为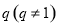
的等比数列. 记
.
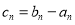（1）求证: 数列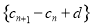
为等比数列；
（2）已知数列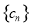
的前
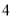项分别为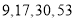
.
①求数列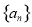和
的通项公式；
②是否存在元素均为正整数的集合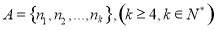
，使得数列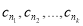
等差数列？证明你的结论.
查看答案和解析>>
科目：高中数学 来源：2017届江苏泰州中学高三上学期期中数学试卷（解析版） 题型：填空题
已知函数
在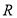
上单调递减，且关于
的方程
恰好有两个不相等的实数解，则
的取值范围是_________.
查看答案和解析>>
科目：高中数学 来源：2017届江苏如东高级中学高三上学情调研二数学试卷（解析版） 题型：解答题
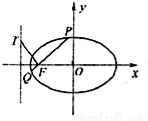
已知椭圆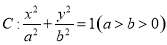
的焦距为4，其短轴的两个端点与长轴的一个端点构成正三角形．
（1）求椭圆
的标准方程；
（2）设
为椭圆
的左焦点，
为左准线
上任意一点，过
作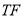
的垂线交椭圆
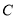于点
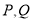，当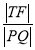
最小时，求点
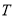的坐标．
查看答案和解析>>
科目：高中数学 来源：2017届河北衡水中学高三理上学期四调考试数学试卷（解析版） 题型：选择题
德国著名数学家狄利克雷在数学领域成就显著，以其名命名的函数
，称为狄利克雷函数，则关于函数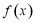
有以下四个命题：
①
；
②函数
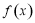是偶函数；
③任意一个非零有理数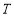
，
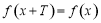对任意
恒成立；
④存在三个点
，使得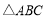
为等边三角形.
其中真命题的个数是（ ）
A．4 B．3 C.2 D．1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
中，
为棱
的中点.
平面
；
平面
.
的定义域为 _________.
，使得
”是假命题，则实数
的取值范围为__________．