
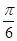 ,求证:FG⊥平面ABCD
,求证:FG⊥平面ABCD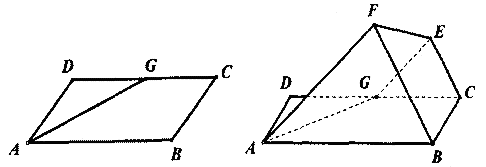
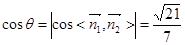 ;(3)见解析.
;(3)见解析.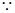 ABCD是平行四边形,
ABCD是平行四边形, CG//AB CG//平面ABF GE//AF GE//平面ABF
CG//AB CG//平面ABF GE//AF GE//平面ABF 平面CEG//平面ABF
平面CEG//平面ABF  CE//平面ABF
CE//平面ABF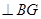 ,如图建立空间直角坐标系
,如图建立空间直角坐标系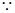 ABCD是平行四边形,
ABCD是平行四边形, CG//AB CG//平面ABF GE//AF GE//平面ABF
CG//AB CG//平面ABF GE//AF GE//平面ABF 平面CEG//平面ABF
平面CEG//平面ABF  CE//平面ABF …………4分
CE//平面ABF …………4分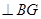 ,如图建立空间直角坐标系
,如图建立空间直角坐标系 则
则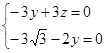
 平面AEF的法向量
平面AEF的法向量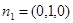

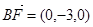
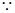
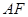 与平面ABCD所成的角为30゜,AF=6
与平面ABCD所成的角为30゜,AF=6  设F(x,y,3)
设F(x,y,3)
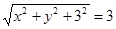

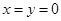
 F(0,0,3)
F(0,0,3) GF=(0,0,3)
GF=(0,0,3) GF
GF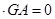
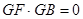

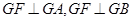

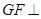 平面ABCD
平面ABCD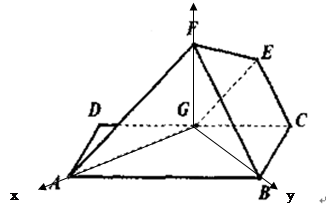
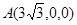
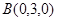
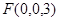
 平面AEF的法向量
平面AEF的法向量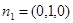

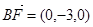
 则
则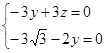

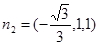

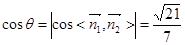 即为所求。……………10分
即为所求。……………10分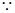
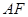 与平面ABCD所成的角为30゜,AF=6
与平面ABCD所成的角为30゜,AF=6  设F(x,y,3)
设F(x,y,3)
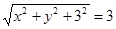

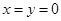
 F(0,0,3)
F(0,0,3) GF=(0,0,3)
GF=(0,0,3) GF
GF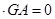
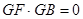

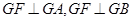

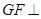 平面ABCD…………15分
平面ABCD…………15分

 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:不详 题型:解答题
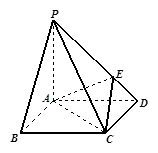
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 的正方形,且PD=
的正方形,且PD= ,PA=PC=
,PA=PC=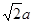 .
.
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
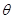 的值;若不能确定,说明理由.
的值;若不能确定,说明理由.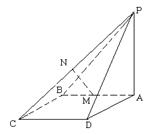
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
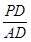 =
=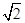 ,求平面PBE与平面ABCD所成的锐二面角的大小.
,求平面PBE与平面ABCD所成的锐二面角的大小.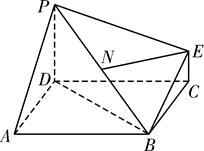
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com