在等差数列{an}中,Sn为数列{an}的前n项和,a7=-2,a20=-28
(1)求通项an
(2)求Sn的最大值.
解:(1)由题意可得等差数列{a
n}的公差d=
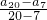
=
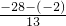
=-2,
故可得a
1=a
7-6d=-2-6×(-2)=10,
故可得数列的通项a
n=a
1+(n-1)d=10-2(n-1)=-2n+12
(2)由(1)可知a
n=-2n+12,a
1=10,令a
n=-2n+12≤0可得n≥6,
故等差数列{a
n}的前5项均为正数,第6项为0,从第7项开始为负值,
故数列的前5项,或前6项和最大,且最大值为S
6=S
5=5a
1+
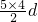
=50-20=30
分析:(1)可得数列的公差d,进而可得首项a
1,代入可得其通项a
n;
(2)令a
n≤0可得n的取值范围,进而可得该数列的前5项均为正数,第6项为0,从第7项开始为负值,从而可得当n=5或时S
n取最大值,由求和公式求解即可.
点评:本题考查等差数列的前n项和公式和通项公式,属基础题.

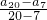 =
=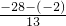 =-2,
=-2,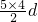 =50-20=30
=50-20=30

 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案