
分析 (Ⅰ)由题意可知$\left\{\begin{array}{l}{2a×\frac{1}{2}=2b}\\{a-c=2-\sqrt{3}}\\{{a}^{2}={b}^{2}+{c}^{2}}\end{array}\right.$,解得a,b即可.
(Ⅱ)将直线l:y=x+m与椭圆C的方程x2+4y2-4=0联立可得:5x2+8mx+4m2-4=0,再由根的判别式和韦达定理进行求解.
解答 解:(Ⅰ)由题意可知$\left\{\begin{array}{l}{2a×\frac{1}{2}=2b}\\{a-c=2-\sqrt{3}}\\{{a}^{2}={b}^{2}+{c}^{2}}\end{array}\right.$,解得a=2,b=1,c=$\sqrt{3}$,
∴椭圆C的方程的方程为:$\frac{{x}^{2}}{4}+{y}^{2}=1$.
(Ⅱ)将线l:y=x+m与椭圆C的方程x2+4y2-4=0联立可得:5x2+8mx+4m2-4=0,
由△=64m2-4×5×(4m2-4)>0,⇒m2<5;
x1+x2=-$\frac{8m}{5}$,x1x2=$\frac{4{m}^{2}-4}{5}$.
|AB|=$\sqrt{1+{1}^{2}}•\sqrt{({x}_{1}+{x}_{2})^{2}-4{x}_{1}{x}_{2}}$=$\frac{4\sqrt{2}•\sqrt{5-{m}^{2}}}{5}$,
原点O到直线l:y=x+m的距离d=$\frac{|m|}{\sqrt{2}}$,
△AOB的面积为s=$\frac{1}{2}$×d×|AB|=$\frac{4\sqrt{2}•\sqrt{5-{m}^{2}}}{5}×\frac{|d|}{5}$=1;
化简得4m4-20m2+25=0,m2=$\frac{5}{2}$,
m=±$\frac{\sqrt{10}}{2}$,直线l的方程为:y=x±$\frac{\sqrt{10}}{2}$
点评 考查椭圆的方程和性质,考查直线方程和椭圆方程联立,消去未知数,运用韦达定理和距离公式,属于中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
| A. | {2,4,5} | B. | {1,2,4,5} | C. | {2,5} | D. | {0,2,3,4,5} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
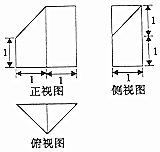
| A. | $\frac{9}{2}$+4$\sqrt{2}$ | B. | 5$+4\sqrt{2}$ | C. | 6$+4\sqrt{2}$ | D. | $\frac{13}{2}$$+4\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 12 | B. | 9 | C. | 8 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 偶函数,且在(0,+∞)上是增函数 | |
| B. | 偶函数,且在(0,+∞)上是减函数 | |
| C. | 奇函数,且在(0,+∞)上是增函数 | |
| D. | 非奇非偶函数,且在(0,+∞)上是增函数 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com