
 ,半径OA为1Km,为了便于游客观光休闲,拟在观光区内铺设一条从入口A到出口B的观光道路,道路由圆弧AC、线段CD及线段BD组成.其中D在线段OB上,且CD∥AO,设∠AOC=θ,
,半径OA为1Km,为了便于游客观光休闲,拟在观光区内铺设一条从入口A到出口B的观光道路,道路由圆弧AC、线段CD及线段BD组成.其中D在线段OB上,且CD∥AO,设∠AOC=θ,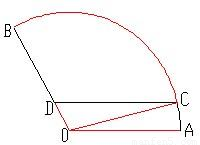
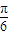 时,观光道路最长..
时,观光道路最长..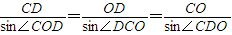 ,又CD∥AO,CO=1,∠AOC=θ,所以
,又CD∥AO,CO=1,∠AOC=θ,所以
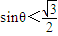 ,所以
,所以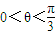 ,所以
,所以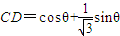 ,θ的取值范围为
,θ的取值范围为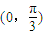
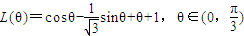 ,
,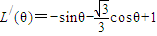
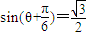 ,又
,又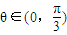 ,所以
,所以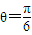
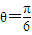 时,L(θ)取到最大值,即θ=
时,L(θ)取到最大值,即θ=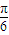 时,观光道路最长.
时,观光道路最长.

科目:高中数学 来源: 题型:
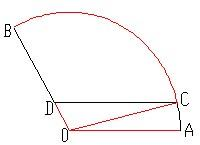 如图扇形AOB是一个观光区的平面示意图,其中∠AOB的圆心角为
如图扇形AOB是一个观光区的平面示意图,其中∠AOB的圆心角为| 2π | 3 |
查看答案和解析>>
科目:高中数学 来源:2010-2011学年江苏省南京市高三第二次模拟考试数学卷 题型:解答题
如图扇形AOB是一个观光区的平面示意图,其中∠AOB的圆心角为 ,半径OA为1Km,为了便于游客观光休闲,拟在观光区内铺设一条从入口A到出口B的观光道路,道路由圆弧AC、线段CD及线段BD组成。其中D在线段OB上,且CD//AO,设∠AOC=θ,
,半径OA为1Km,为了便于游客观光休闲,拟在观光区内铺设一条从入口A到出口B的观光道路,道路由圆弧AC、线段CD及线段BD组成。其中D在线段OB上,且CD//AO,设∠AOC=θ,
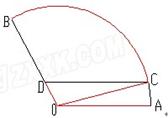
(1)用θ表示CD的长度,并写出θ的取值范围。
(2)当θ为何值时,观光道路最长?
查看答案和解析>>
科目:高中数学 来源:江苏模拟题 题型:解答题
 ,半径OA为1km。为了便于游客观光休闲,拟在观光区内铺设一条从入口A到出口B的观光道路,道路由弧AC、线段CD及线段BD组成,其中D在线段OB上,且CD∥AO,设∠AOC=θ,
,半径OA为1km。为了便于游客观光休闲,拟在观光区内铺设一条从入口A到出口B的观光道路,道路由弧AC、线段CD及线段BD组成,其中D在线段OB上,且CD∥AO,设∠AOC=θ,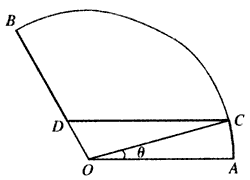
查看答案和解析>>
科目:高中数学 来源:2011年广东省高考数学模拟试卷3(理科)(解析版) 题型:解答题
 ,半径OA为1Km,为了便于游客观光休闲,拟在观光区内铺设一条从入口A到出口B的观光道路,道路由圆弧AC、线段CD及线段BD组成.其中D在线段OB上,且CD∥AO,设∠AOC=θ,
,半径OA为1Km,为了便于游客观光休闲,拟在观光区内铺设一条从入口A到出口B的观光道路,道路由圆弧AC、线段CD及线段BD组成.其中D在线段OB上,且CD∥AO,设∠AOC=θ,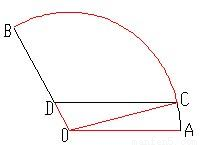
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com