【题目】如图，上海迪士尼乐园将一三角形地块ABC的一角APQ开辟为游客体验活动区．已知∠A=120°，AB、AC的长度均大于200米．设AP=x，AQ=y，且AP，AQ总长度为200米．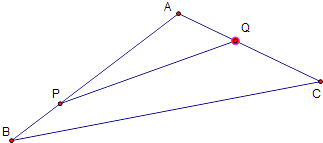 
（1）当x，y为何值时？游客体验活动区APQ的面积最大，并求最大面积；
（2）当x，y为何值时？线段|PQ|最小，并求最小值．
【答案】
（1）解：因为：AP=x，AQ=y且x+y=200
所以： 
．
当且仅当x=y=100时，等号成立．
所以：当x=y=100米时， 
平方米
（2）解：因为：PQ2=x2+y2﹣2xycos120°
=x2+y2+xy…8分
=x2+（200﹣x）2+x（200﹣x）
=x2﹣200x+40000
=（x﹣100）2+30000．
所以：当x=100米，线段 
米，此时，y=100米
【解析】（1）由已知利用三角形面积公式，基本不等式可得 ，即可得解．（2）利用已知及余弦定理可得PQ2=x2+y2﹣2xycos120°=（x﹣100）2+30000，根据二次函数的图象和性质即可解得线段|PQ|最小值．
【考点精析】通过灵活运用正弦定理的定义和余弦定理的定义，掌握正弦定理:
；余弦定理:
;
;
即可以解答此题．
科目：高中数学 来源： 题型：
【题目】下列命题中正确的命题个数是 ( )
①. 如果
共面， 
也共面,则
共面;
②.已知直线a的方向向量
与平面
，若
// 
，则直线a// 
;
③若
共面，则存在唯一实数
使
,反之也成立;
④.对空间任意点O与不共线的三点A、B、C，若
=x
+y
+z
（其中x、y、z∈R），则P、A、B、C四点共面
A. 3 B. 2 C. 1 D. 0
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知向量 
=（sinx， 
）， 
=（cosx，﹣1）．
（1）当 ∥ 时，求tan（x﹣ 
）的值；
（2）设函数f（x）=2（ + ） ，当x∈[0， 
]时，求f（x）的值域．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数
，
．
（1）若函数
是奇函数，求实数
的值；
（2）在在（1）的条件下，判断函数
与函数
的图像公共点个数，并说明理由；
（3）当
时，函数
的图象始终在函数
的图象上方，求实数的取值范围．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数f（x）=ax+ 
+2﹣2a（a＞0）的图象在点（1，f（1））处的切线与直线y=2x+1平行．
（1）求a，b满足的关系式；
（2）若f（x）≥2lnx在[1，+∞）上恒成立，求a的取值范围；
（3）证明：1+ 
+ 
+…+ 
＞ 
（2n+1）+ 
（n∈N*）．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，将一副三角板拼接，使它们有公共边BC，且使两个三角形所在的平面互相垂直，若
∠BAC＝90°，AB＝AC，∠CBD＝90°，∠BDC＝60°，BC＝6。
⑴ 求证：平面
平面ACD；
⑵ 求二面角
的平面角的正切值；
⑶ 设过直线AD且与BC平行的平面为
，求点B到平面的距离。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
