
分析 (Ⅰ)由椭圆的离心率公式求得a和b的关系,将(-$\sqrt{3}$,$\frac{\sqrt{2}}{2}$)代入椭圆方程,即可求得a和b的值,求得椭圆方程;
(Ⅱ)将直线方程代入椭圆方程,求得P的横坐标,求得丨BP丨,利用直线垂直的斜率关系求得丨BQ丨,由$\frac{|BP|}{|BQ|}$=$\frac{1}{2}$,根据函数零点的判断即可存在k∈R,$\frac{|BP|}{|BQ|}$=$\frac{1}{2}$.
解答 解:(Ⅰ)椭圆的离心率e=$\frac{c}{a}$=$\sqrt{1-\frac{{b}^{2}}{{a}^{2}}}$=$\frac{\sqrt{2}}{2}$,则a2=2b2,
将点(-$\sqrt{3}$,$\frac{\sqrt{2}}{2}$)代入椭圆方程$\frac{3}{{a}^{2}}+\frac{1}{2{b}^{2}}=1$,解得:a2=4,b2=2,
∴椭圆的标准方程为:$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{2}=1$,
(Ⅱ)由题意的对称性可知:设存在存在k>0,使得$\frac{|BP|}{|BQ|}$=$\frac{1}{2}$,
由a2=2b2,椭圆方程为:$\frac{{x}^{2}}{2{b}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1$,
将直线方程代入椭圆方程,整理得:(1+2k2)x2+4kbx=0,
解得:xP=-$\frac{4kb}{1+2{k}^{2}}$,则丨BP丨=$\sqrt{1+{k}^{2}}$×$\frac{4kb}{1+2{k}^{2}}$,
由BP⊥BQ,则丨BQ丨=$\sqrt{1+(-\frac{1}{k})^{2}}$×丨$\frac{4(-\frac{1}{k})b}{1+2(-\frac{1}{k})^{2}}$丨=$\sqrt{1+{k}^{2}}$•$\frac{4b}{{k}^{2}+2}$,
由$\frac{|BP|}{|BQ|}$=$\frac{1}{2}$.,则2$\sqrt{1+{k}^{2}}$×$\frac{4kb}{1+2{k}^{2}}$=$\sqrt{1+{k}^{2}}$•$\frac{4b}{{k}^{2}+2}$,
整理得:2k3-2k2+4k-1=0,
设f(x)=2k3-2k2+4k-1,由f($\frac{1}{4}$)<0,f($\frac{1}{2}$)>0,
∴函数f(x)存在零点,
∴存在k∈R,$\frac{|BP|}{|BQ|}$=$\frac{1}{2}$.
点评 本题考查椭圆的标准方程及椭圆的离心率,考查直线与椭圆的位置关系,弦长公式,考查函数零点的判断,考查计算能力,属于中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题

| A. | $S=\frac{100}{101},P=\frac{100}{101}$ | B. | $S=\frac{99}{100},P=\frac{99}{202}$ | ||
| C. | $S=\frac{100}{101},P=\frac{99}{202}$ | D. | $S=\frac{100}{101},P=\frac{99}{100}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 如图,已知正方体ABC-A1B1C1D1中,AB=a,P为线段BC1上一点,Q为平面ABCD内一点,则D1P+PQ的最小值为(1+$\frac{\sqrt{2}}{2}$)a.
如图,已知正方体ABC-A1B1C1D1中,AB=a,P为线段BC1上一点,Q为平面ABCD内一点,则D1P+PQ的最小值为(1+$\frac{\sqrt{2}}{2}$)a.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在三棱锥ABC-A1B1C1中,△ABC是边长为2的等边三角形,AA1=4,A1在底面ABC上的射影为BC的中点E,D是B1C1的中点.
如图,在三棱锥ABC-A1B1C1中,△ABC是边长为2的等边三角形,AA1=4,A1在底面ABC上的射影为BC的中点E,D是B1C1的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 9 | B. | 3 | C. | $\sqrt{109}$ | D. | 3$\sqrt{10}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {0,1,2} | B. | {1,2} | C. | {0} | D. | {0,1} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
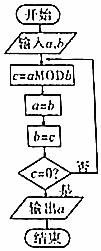 “欧几里得算法”是有记载的最古老的算法,可追溯至公元前300年前,如图的程序框图的算法思路就是来源于“欧几里得算法”.执行改程序框图(图中“aMODb”表示a除以b的余数),若输入的a,b分别为675,125,则输出的a=( )
“欧几里得算法”是有记载的最古老的算法,可追溯至公元前300年前,如图的程序框图的算法思路就是来源于“欧几里得算法”.执行改程序框图(图中“aMODb”表示a除以b的余数),若输入的a,b分别为675,125,则输出的a=( )| A. | 0 | B. | 25 | C. | 50 | D. | 75 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com