
| π |
| 6 |
| 3 |
| 3 |
| π |
| 6 |
| π |
| 6 |
| 3 |
| 3 |
| 3 |
| 3 |


科目:高中数学 来源: 题型:
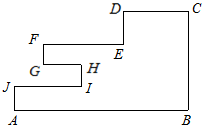 (2008•深圳二模)一个质点从A出发依次沿图中线段到达B、C、D、E、F、G、H、I、J各点,最后又回到A(如图所示),其中:AB⊥BC,AB∥CD∥EF∥HG∥IJ,BC∥DE∥FG∥HI∥JA.欲知此质点所走路程,至少需要测量n条线段的长度,则n=( )
(2008•深圳二模)一个质点从A出发依次沿图中线段到达B、C、D、E、F、G、H、I、J各点,最后又回到A(如图所示),其中:AB⊥BC,AB∥CD∥EF∥HG∥IJ,BC∥DE∥FG∥HI∥JA.欲知此质点所走路程,至少需要测量n条线段的长度,则n=( )查看答案和解析>>
科目:高中数学 来源: 题型:
 (2008•深圳二模)当点M(x,y)在如图所示的三角形ABC内(含边界)运动时,目标函数z=kx+y取得最大值的一个最优解为(1,2),则实数k的取值范围是( )
(2008•深圳二模)当点M(x,y)在如图所示的三角形ABC内(含边界)运动时,目标函数z=kx+y取得最大值的一个最优解为(1,2),则实数k的取值范围是( )查看答案和解析>>
科目:高中数学 来源: 题型:
| (4n+6)an+4n+10 |
| 2n+1 |
| an+2 |
| 2n+1 |
| 1 |
| S3 |
| 1 |
| S4 |
| 1 |
| Sn |
| 1 |
| 10 |
查看答案和解析>>
科目:高中数学 来源: 题型:
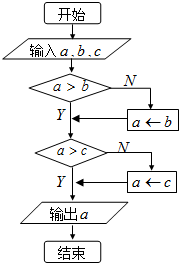 (2008•深圳二模)如图所示的算法中,令a=tanθ,b=sinθ,c=cosθ,若在集合{θ| -
(2008•深圳二模)如图所示的算法中,令a=tanθ,b=sinθ,c=cosθ,若在集合{θ| -| π |
| 4 |
| 3π |
| 4 |
| π |
| 4 |
| π |
| 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com