
【题目】设数列{an}的前n项和为Sn , 满足Sn=2nan+1﹣3n2﹣4n,n∈N* , 且S3=15.
(1)求a1 , a2 , a3的值;
(2)求数列{an}的通项公式.
【答案】
(1)
解:由Sn=2nan+1﹣3n2﹣4n,n∈N*,得:
S2=4a3﹣20 ①
又S3=S2+a3=15 ②
联立①②解得:a3=7.
再在Sn=2nan+1﹣3n2﹣4n中取n=1,得:
a1=2a2﹣7 ③
又S3=a1+a2+7=15 ④
联立③④得:a2=5,a1=3.
∴a1,a2,a3的值分别为3,5,7
(2)
解:∵a1=3=2×1+1,a2=5=2×2+1,a3=7=2×3+1.
由此猜测an=2n+1.
下面由数学归纳法证明:
①当n=1时,a1=3=2×1+1成立.
②假设n=k时结论成立,即ak=2k+1.
那么,当n=k+1时,
由Sn=2nan+1﹣3n2﹣4n,得 ![]() ,
,
![]() ,
,
两式作差得: ![]() .
.
∴ ![]()
= ![]() =2(k+1)+1.
=2(k+1)+1.
综上,当n=k+1时结论成立.
∴an=2n+1.
【解析】(1)在数列递推式中取n=2得一关系式,再把S3变为S2+a3得另一关系式,联立可求a3 , 然后把递推式中n取1,再结合S3=15联立方程组求得a1 , a2;(2)由(1)中求得的a1 , a2 , a3的值猜测出数列的一个通项公式,然后利用数学归纳法证明.
【考点精析】关于本题考查的数列的通项公式,需要了解如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式才能得出正确答案.


科目:高中数学 来源: 题型:
【题目】某零售店近5个月的销售额和利润额资料如下表:
商店名称 |
|
|
|
|
|
销售额 | 3 | 5 | 6 | 7 | 9 |
利润额 | 2 | 3 | 3 | 4 | 5 |
(1)画出散点图.观察散点图,说明两个变量有怎样的相关关系;
(2)用最小二乘法计算利润额![]() 关于销售额
关于销售额![]() 的回归直线方程;
的回归直线方程;
(3)当销售额为4千万元时,利用(2)的结论估计该零售店的利润额(百万元).
[参考公式: ,
,![]() ]
]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,![]() 是平行四边形,
是平行四边形,![]() ,
,![]() 为
为![]() 的中点,且有
的中点,且有![]() ,现以
,现以![]() 为折痕,将
为折痕,将![]() 折起,使得点
折起,使得点![]() 到达点
到达点![]() 的位置,且
的位置,且![]()
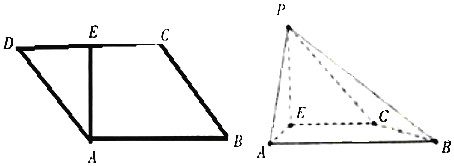
(1)证明:![]() 平面
平面![]() ;
;
(2)若四棱锥![]() 的体积为
的体积为![]() ,求四棱锥
,求四棱锥![]() 的侧面积.
的侧面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 的前n项和
的前n项和![]() .
.
![]() 若三角形的三边长分别为
若三角形的三边长分别为![]() ,
,![]() ,
,![]() ,求此三角形的面积;
,求此三角形的面积;
![]() 探究数列
探究数列![]() 中是否存在相邻的三项,同时满足以下两个条件:
中是否存在相邻的三项,同时满足以下两个条件:![]() 此三项可作为三角形三边的长;
此三项可作为三角形三边的长;![]() 此三项构成的三角形最大角是最小角的2倍
此三项构成的三角形最大角是最小角的2倍![]() 若存在,找出这样的三项,若不存在,说明理由.
若存在,找出这样的三项,若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列三个命题中
①“k=1”是“函数y=cos2kx-sin2kx的最小正周期为π”的充要条件;
②“a=3”是“直线ax+2y+3a=0与直线3x+(a-1)y=a-7相互垂直”的充要条件;
③“双曲线![]() 上任意点M到两条渐近线距离的积为定值”的逆否命题
上任意点M到两条渐近线距离的积为定值”的逆否命题
其中是真命题的为________
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)= ![]() ,其中k<﹣2.
,其中k<﹣2.
(1)求函数f(x)的定义域D(用区间表示);
(2)讨论函数f(x)在D上的单调性;
(3)若k<﹣6,求D上满足条件f(x)>f(1)的x的集合(用区间表示).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某厂家为了了解某新产品使用者的年龄情况,现随机调査100 位使用者的年龄整理后画出的频率分布直方图如图所示.

(1)求100名使用者中各年龄组的人数,并利用所给的频率分布直方图估计所有使用者的平均年龄;
(2)若已从年龄在![]() 的使用者中利用分层抽样选取了6人,再从这6人中选出2人,求这2人在不同的年龄组的概率.
的使用者中利用分层抽样选取了6人,再从这6人中选出2人,求这2人在不同的年龄组的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一位数学老师在黑板上写了三个向量![]() ,
,![]() ,
,![]() ,其中
,其中![]() ,
,![]() 都是给定的整数.老师问三位学生这三个向量的关系,甲回答:“
都是给定的整数.老师问三位学生这三个向量的关系,甲回答:“![]() 与
与![]() 平行,且
平行,且![]() 与
与![]() 垂直”,乙回答:“
垂直”,乙回答:“![]() 与
与![]() 平行”,丙回答:“
平行”,丙回答:“![]() 与
与![]() 不垂直也不平行”,最后老师发现只有一位学生判断正确,由此猜测
不垂直也不平行”,最后老师发现只有一位学生判断正确,由此猜测![]() ,
,![]() 的值不可能为( )
的值不可能为( )
A. ![]() ,
,![]() B.
B. ![]() ,
,![]() C.
C. ![]() ,
,![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com