
如图,摩天轮的半径为50 m,点O距地面的高度为60 m,摩天轮做匀速转动,每3 min转一圈,摩天轮上点P的起始位置在最低点处.
(1)试确定在时刻t(min)时点P距离地面的高度;
(2)在摩天轮转动的一圈内,有多长时间点P距离地面超过85 m?
(1) y=60-50cos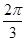 t (t≥0) (2) 在摩天轮转动的一圈内,点P距离地面超过85 m的时间有1分钟.
t (t≥0) (2) 在摩天轮转动的一圈内,点P距离地面超过85 m的时间有1分钟.
解析试题分析:(1)解:设点P离地面的距离为y,则可令 y=Asin(ωt+φ)+b.
由题设可知A=50,b=60. 2分
又T=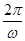 =3,所以ω=
=3,所以ω=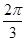 ,从而y=50sin(
,从而y=50sin(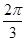 t+φ)+60. 4分
t+φ)+60. 4分
再由题设知t=0时y=10,代入y=50sin(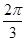 t+φ)+60,得sinφ=-1,从而φ=-
t+φ)+60,得sinφ=-1,从而φ=-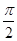 .
.
6分
因此,y=60-50cos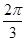 t (t≥0). 8分
t (t≥0). 8分
(2)要使点P距离地面超过85 m,则有y=60-50cos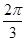 t>85,即cos
t>85,即cos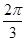 t<-
t<- .
.
10分
于是由三角函数基本性质推得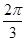 <
<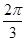 t<
t<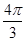 ,即1<t<2. 12分
,即1<t<2. 12分
所以,在摩天轮转动的一圈内,点P距离地面超过85 m的时间有1分钟.
14分
考点:三角函数的运用
点评:解决的关键是利用摩天轮的转动有周期性,以及点的坐标的表示来得到解析式,属于基础题。


科目:高中数学 来源: 题型:解答题
如图所示,在 △ABC内有一内接正方形,它的一条边在斜边BC上,设AB=
△ABC内有一内接正方形,它的一条边在斜边BC上,设AB= ,∠ABC
,∠ABC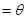

(1)求△ABC的面积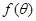 与正方形面积
与正方形面积 ;
;
(2)当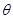 变化时,求
变化时,求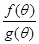 的最小值,并求出对应
的最小值,并求出对应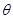 的值。
的值。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com