(12分)已知函数
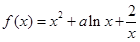
在
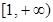
上是单调递增函数,求实数
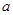
的取值范围.
试题分析:由
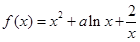
,得
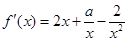
. ……4分
若函数
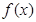
为
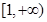
上的单调增函数,则
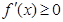
在
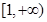
上恒成立,
即不等式
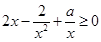
在
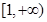
上恒成立.
也即
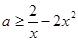
在
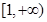
上恒成立. ……8分
又
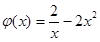
在
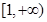
上为减函数,
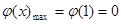
.
所以
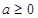
. ……12分
点评:函数是单调增函数,可知
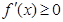
恒成立,而不是
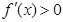
恒成立,而恒成立问题往往转化成最值问题解决.
练习册系列答案
相关习题
科目:高中数学
来源:不详
题型:解答题
(本小题满分14分)已知函数
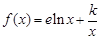
(其中
e是自然对数的底数,
k为正数)
(1)若

在
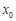
处取得极值,且
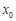
是

的一个零点,求
k的值;
(2)若
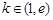
,求

在区间
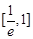
上的最大值.
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
(本小题满分13分)
已知函数

(1)判断
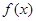
的单调性;
(2)记
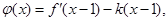
若函数
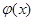
有两个零点

,求证
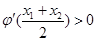
查看答案和解析>>
科目:高中数学
来源:不详
题型:单选题
某物体的位移
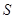
(米)与时间
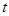
(秒)的关系是
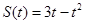
,则物体在
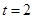
秒时的瞬时速度为( )
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
(本题满分12分)
求下列函数的导数
(1)
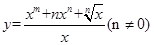
(2)
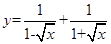
查看答案和解析>>
科目:高中数学
来源:不详
题型:单选题
已知定义在
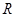
上的函数
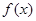
满足
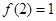
,且
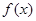
的导函数
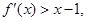
则不等式
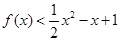
的解集为( )
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
(本小题满分14分)已知函数
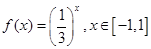
,函数
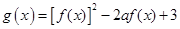
的最小值为
,
(1)当
时,求
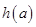
(2)是否存在实数
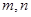
同时满足下列条件:①
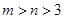
;②当
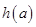
的定义域为
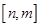
时,值域为
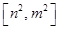

?若存在,求出
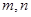
的值;若不存在,请说明理由。
查看答案和解析>>
科目:高中数学
来源:不详
题型:单选题
直线y =" 2x" + 1与曲线
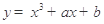
相切于点A(1,3)则b的值为
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
(本小题满分10分)(1)求函数
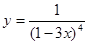
的导数.
(2)求函数f(x)=
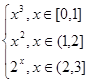
在区间[0,3]上的积分.
查看答案和解析>>

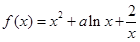 在
在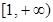 上是单调递增函数,求实数
上是单调递增函数,求实数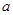 的取值范围.
的取值范围. 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案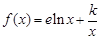 (其中e是自然对数的底数,k为正数)
(其中e是自然对数的底数,k为正数) 在
在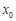 处取得极值,且
处取得极值,且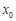 是
是 的一个零点,求k的值;
的一个零点,求k的值;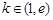 ,求
,求 在区间
在区间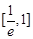 上的最大值.
上的最大值.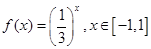 ,函数
,函数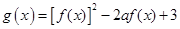 的最小值为
的最小值为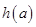 ,
,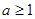 时,求
时,求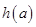
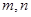 同时满足下列条件:①
同时满足下列条件:①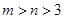 ;②当
;②当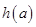 的定义域为
的定义域为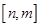 时,值域为
时,值域为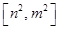
 ?若存在,求出
?若存在,求出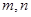 的值;若不存在,请说明理由。
的值;若不存在,请说明理由。