
【题目】已知 ![]() =(2,﹣
=(2,﹣ ![]() ),
), ![]() =(sin2(
=(sin2( ![]() +x),cos2x).令f(x)=
+x),cos2x).令f(x)= ![]()
![]() ﹣1,x∈R,函数g(x)=f(x+φ),φ∈(0,
﹣1,x∈R,函数g(x)=f(x+φ),φ∈(0, ![]() )的图象关于(﹣
)的图象关于(﹣ ![]() ,0)对称. (Ⅰ) 求f(x)的解析式,并求φ的值;
,0)对称. (Ⅰ) 求f(x)的解析式,并求φ的值;
(Ⅱ)在△ABC中sinC+cosC=1﹣ ![]() ,求g(B)的取值范围.
,求g(B)的取值范围.
科目:高中数学 来源: 题型:
【题目】某市有A、B两家羽毛球球俱乐部,两家设备和服务都很好,但收费方式不同,A俱乐部每块场地每小时收费6元;B俱乐部按月计费,一个月中20小时以内![]() 含20小时
含20小时![]() 每块场地收费90元,超过20小时的部分,每块场地每小时2元,某企业准备下个月从这两家俱乐部中的一家租用一块场地开展活动,其活动时间不少于12小时,也不超过30小时.
每块场地收费90元,超过20小时的部分,每块场地每小时2元,某企业准备下个月从这两家俱乐部中的一家租用一块场地开展活动,其活动时间不少于12小时,也不超过30小时.
![]() 设在A俱乐部租一块场地开展活动x小时的收费为
设在A俱乐部租一块场地开展活动x小时的收费为![]() 元
元![]() ,在B俱乐部租一块场地开展活动x小时的收费为
,在B俱乐部租一块场地开展活动x小时的收费为![]() 元
元![]() ,试求
,试求![]() 与
与![]() 的解析式;
的解析式;
![]() 问该企业选择哪家俱乐部比较合算,为什么?
问该企业选择哪家俱乐部比较合算,为什么?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
, ![]() ,函数
,函数![]() 的图象在点
的图象在点![]() 处的切线平行于
处的切线平行于![]() 轴.
轴.
(1)求![]() 的值;
的值;
(2)求函数![]() 的极小值;
的极小值;
(3)设斜率为![]() 的直线与函数
的直线与函数![]() 的图象交于两点
的图象交于两点![]() ,
, ![]() ,
, ![]() ,证明:
,证明: ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校餐厅新推出A、B、C、D四款套餐,某一天四款套餐销售情况的条形图如下.为了了解同学对新推出的四款套餐的评价,对每位同学都进行了问卷调查,然后用分层抽样的方法从调查问卷中抽取20份进行统计,统计结果如下面表格所示:
满意 | 一般 | 不满意 | |
A套餐 | 50% | 25% | 25% |
B套餐 | 80% | 0 | 20% |
C套餐 | 50% | 50% | 0 |
D套餐 | 40% | 20% | 40% |
(Ⅰ)若同学甲选择的是A款套餐,求甲的调查问卷被选中的概率;
(Ⅱ)若想从调查问卷被选中且填写不满意的同学中再选出2人进行面谈,求这两人中至少有一人选择的是D款套餐的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆C的圆心在直线上![]() ,且与直线
,且与直线![]() 相切于点
相切于点![]()
(1)求圆C的方程;
(2)是否存在过点![]() 的直线
的直线![]() 与圆C交于
与圆C交于![]() 两点,且
两点,且![]() 的面积为
的面积为![]() (O为坐标原点),若存在,求出直线
(O为坐标原点),若存在,求出直线![]() 的方程,若不存在,请说明理由.
的方程,若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在多面体ABCDFE中,四边形ABCD是矩形,AB∥EF,AB=2EF,∠EAB=90°,平面ABFE⊥平面ABCD.
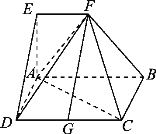
(1)若G点是DC的中点,求证:FG∥平面AED.
(2)求证:平面DAF⊥平面BAF.
(3)若AE=AD=1,AB=2,求三棱锥D-AFC的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】综合题。
(1)设不等式(x﹣a)(x+a﹣2)<0的解集为N, ![]() ,若x∈N是x∈M的必要条件,求a的取值范围.
,若x∈N是x∈M的必要条件,求a的取值范围.
(2)已知命题:“x∈{x|﹣1<x<1},使等式x2﹣x﹣m=0成立”是真命题,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业投入81万元经销某产品,经销时间共60个月,市场调研表明,该企业在经销这个产品期间第x个月的利润 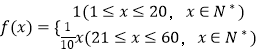 (单位:万元),为了获得更多的利润,企业将每月获得的利润投入到次月的经营中,记第x个月的当月利润率
(单位:万元),为了获得更多的利润,企业将每月获得的利润投入到次月的经营中,记第x个月的当月利润率 ![]() ,例如:
,例如: ![]() .
.
(1)求g(10);
(2)求第x个月的当月利润率g(x);
(3)该企业经销此产品期间,哪个月的当月利润率最大,并求该月的当月利润率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]()
![]() .
.
(1)当![]() 时,求函数
时,求函数![]() 的极小值;
的极小值;
(2)若函数![]() 在
在![]() 有
有![]() 个零点,求实数
个零点,求实数![]() 的取值范围;
的取值范围;
(3)在(2)的条件下,若函数![]() 在
在![]() 的三个零点分别为
的三个零点分别为![]() ,求证:
,求证: ![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com