练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
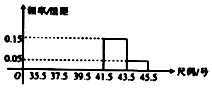
    12．某商场为了了解某日旅游鞋的销售情况，抽取了部分顾客所购鞋的尺寸，将所得数据整理后，画出频率分布直方图如图所示．已知从左到右前3个小组的频率之比为1：2：3，第4小组与第5小组的频率分布如图所示，第2小组的频数为10，则第4小组顾客的人数是（　　）
    A．15B．20C．25D．30

    分析 有第四组与第五组的频率和得到前3组的频率和，又根据前三组的频率之比即可得到第二组的频率，结合第二组的频数可得抽取的顾客人数，由此能求出第4小组顾客的人数．

    解答 解：由题意得：第4小组与第5小组的频率分别为0.15×2=0.3和0.05×2=0.1，
    所以前3组的频率和为0.6．
    又因为从左至右前3个小组的频率之比为1：2：3，
    所以从左至右第2个小组的频率为：0.2．
    因为第二小组的频数为10，
    所以抽取的顾客人数是$\frac{10}{0.2}$=50人．
    故第4小组顾客的人数是50×0.3=15．
    故选：A．

    点评 本题主要考查了频率及频率分布直方图，考查运用统计知识解决简单实际问题的能力，数据处理能力和运用意识

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    2．已知函数f（x）=lnx-cx（c∈R）
    （1）讨论函数f（x）的单调性；
    （2）设函数f（x）有两个相异零点x1，x2，求证：${x_1}•{x_2}＞{e^2}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    3．计算（式中各字母均为正数）
    （1）$（\frac{{8{s^6}{t^{-3}}}}{{125{r^9}}}{）^{-\frac{2}{3}}}$
    （2）$（3{x^{\frac{1}{4}}}+2{y^{-\frac{1}{2}}}）（3{x^{\frac{1}{4}}}-2{y^{-\frac{1}{2}}}）$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

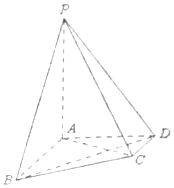    20．在四棱锥P-ABCD中，AB∥CD，AB⊥AD，AB=4，AD=2$\sqrt{2}$，CD=2，PA⊥平面ABCD，PA=4．
    （1）求证：BD⊥平面PAC；
    （2）异面直线PD与AC所成的角．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    7．在极坐标系中，曲线C的方程为$ρ=4（cosθ+sinθ）-\frac{6}{ρ}$，以极点O为原点，极轴为x轴的正半轴建立平面直角坐标系．
    （1）求曲线C的参数方程；
    （2）在直角坐标系中，点M（x，y）是曲线C上一动点，求x+y的最大值，并求此时点M的直角坐标．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    17．已知数列{an}的前n项和为Sn，且2Sn=1-an（n∈N*）．
    （1）求数列{an}的通项公式；
    （2）设${b_n}={log_{\frac{1}{3}}}{a_n}$，记数列{anbn}的前n项和为Tn，求证：Tn＜$\frac{3}{4}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    4．平行六面体ABCD-A'B'C'D'中，若$\overrightarrow{AC'}=x\overrightarrow{AB}+2y\overrightarrow{BC}-3z\overrightarrow{CC'}$，则x+y+z=（　　）
    A．$\frac{7}{6}$B．1C．$\frac{5}{6}$D．$\frac{2}{3}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    1．在△ABC中，$\overrightarrow{AD}•\overrightarrow{BC}=0$，$|{\overrightarrow{AB}}|=3$，$|{\overrightarrow{BC}}|=5$，$\overrightarrow{BD}=\frac{2}{3}\overrightarrow{DC}$，点P满足$\overrightarrow{AP}=λ\overrightarrow{AB}+（{1-λ}）\overrightarrow{AC}$，λ∈R，则$\overrightarrow{AP}•\overrightarrow{AD}$为5．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    2．$\frac{1}{a}＞-1$是a＜-1成立的（　　）
    A．充分不必要条件B．必要不充分条件
    C．充要条件D．既不充分也不必要条件

    查看答案和解析>>

    同步练习册答案