
【题目】如图,五面体![]() 中,四边形
中,四边形![]() 是菱形,
是菱形, ![]() 是边长为2的正三角形,
是边长为2的正三角形, ![]() ,
, ![]() .
.
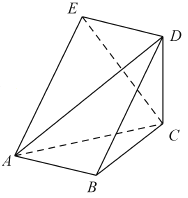
(1)证明: ![]() ;
;
(2)若点![]() 在平面
在平面![]() 内的射影
内的射影![]() ,求
,求![]() 与平面
与平面![]() 所成的角的正弦值.
所成的角的正弦值.
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案科目:高中数学 来源: 题型:
【题目】某市卫生防疫部门为了控制某种病毒的传染,提供了批号分别为![]() 的五批疫苗,供全市所辖的
的五批疫苗,供全市所辖的![]() 三个区市民注射,每个区均能从中任选其中一个批号的疫苗接种.
三个区市民注射,每个区均能从中任选其中一个批号的疫苗接种.
(1)求三个区注射的疫苗批号中恰好有两个区相同的概率;
(2)记![]() 三个区选择的疫苗批号的中位数为
三个区选择的疫苗批号的中位数为![]() ,求
,求 ![]() 的分布列及期望.
的分布列及期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有下列四种说法:
①命题“![]() ”为假,则
”为假,则![]() 、
、![]() 至少一个为假;
至少一个为假;
②命题“一次函数都是单调函数”的否定是“一次函数都不是单调函数”;
③动点![]() 到点
到点![]()
![]() 与到点
与到点![]() 的距离之和为2,则点
的距离之和为2,则点![]() 的轨迹是焦点在
的轨迹是焦点在![]() 轴上的椭圆;
轴上的椭圆;
④命题“若直线与双曲线相切,则该直线与双曲线只有一个公共点”的逆命题是真命题.
其中正确的有__________.(填写序号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】平面内动点P(x,y)与两定点A(-2, 0), B(2,0)连线的斜率之积等于![]() ,若点P的轨迹为曲线E,过点Q
,若点P的轨迹为曲线E,过点Q![]() 作斜率不为零的直线
作斜率不为零的直线![]() 交曲线E于点
交曲线E于点![]() .
.
(I)求曲线E的方程;
(II)求证: ![]() ;
;
(III)求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
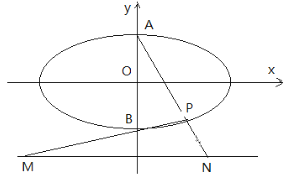
【题目】如图椭圆![]() 的上下顶点为A、B,直线
的上下顶点为A、B,直线![]() :
: ![]() ,点P是椭圆上异于点A、B的任意一点,连结AP并延长交直线
,点P是椭圆上异于点A、B的任意一点,连结AP并延长交直线![]() 于点N,连结BP并延长交直线
于点N,连结BP并延长交直线![]() 于点M,设AP、BP所在直线的斜率分别为
于点M,设AP、BP所在直线的斜率分别为![]() ,若椭圆的离心率为
,若椭圆的离心率为![]() ,且过点
,且过点![]() ,(1)求
,(1)求![]() 的值,并求
的值,并求![]() 最小值;(2)随着点P的变化,以MN为直径的圆是否恒过定点,若过定点,求出该定点坐标;若不过定点,请说明理由。
最小值;(2)随着点P的变化,以MN为直径的圆是否恒过定点,若过定点,求出该定点坐标;若不过定点,请说明理由。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某经销商从外地水产养殖厂购进一批小龙虾,并随机抽取40只进行统计,按重量分类统计结果如下图:

(1)记事件![]() 为:“从这批小龙虾中任取一只,重量不超过35
为:“从这批小龙虾中任取一只,重量不超过35![]() 的小龙虾”,求
的小龙虾”,求![]() 的估计值;
的估计值;
(2)若购进这批小龙虾100千克,试估计这批小龙虾的数量;
(3)为适应市场需求,了解这批小龙虾的口感,该经销商将这40只小龙虾分成三个等级,如下表:
等级 | 一等品 | 二等品 | 三等品 |
重量( |
|
|
|
按分层抽样抽取10只,再随机抽取3只品尝,记![]() 为抽到二等品的数量,求抽到二级品的期望.
为抽到二等品的数量,求抽到二级品的期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() .
.
(1)用定义证明函数f(x)在(﹣∞,+∞)上为减函数;
(2)若x∈[1,2],求函数f(x)的值域;
(3)若g(x)= ![]() ,且当x∈[1,2]时g(x)≥0恒成立,求实数a的取值范围.
,且当x∈[1,2]时g(x)≥0恒成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 是椭圆
是椭圆![]() 的左右焦点,
的左右焦点,![]() 为原点,
为原点,![]()
![]() 在椭圆上,线段
在椭圆上,线段![]() 与
与![]() 轴的交点
轴的交点![]() 满足
满足![]() .
.
(1)求椭圆的标准方程;
(2)过椭圆右焦点![]() 作直线
作直线![]() 交椭圆于
交椭圆于![]() 两点,交
两点,交![]() 轴于
轴于![]() 点,若
点,若![]() ,求
,求![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com