
分析 (1)利用导数求单调区间;
(2)方程f(x)=g(x)在区间[$\sqrt{2}$,e]上有两个不等解?a=$\frac{2lnx}{{x}^{2}}$在区间[$\sqrt{2}$,e]上有两个不等解.
令G(x)=$\frac{2lnx}{{x}^{2}}$,根据G(x)的单调性及图象,求出a的取值范围.
解答 解:(1)当a=1时,F(x)=f(x)-g(x)=x2-2ln x,其定义域为(0,+∞),
∴F′(x)=2x-$\frac{2}{x}$=$\frac{{2({{x^2}-1})}}{x}$(x>0)
当$\frac{{2({{x^2}-1})}}{x}$>0时,x>1; 当$\frac{{2({{x^2}-1})}}{x}$<0时,0<x<1…(4分)
∴当a=1时函数F(x)=f(x)-g(x)的单调递增区间为(1,+∞),单调递减区间为(0,1).
(2)方程f(x)=g(x)在区间[$\sqrt{2}$,e]上有两个不等解?a=$\frac{2lnx}{{x}^{2}}$在区间[$\sqrt{2}$,e]上有两个不等解.
令G(x)=$\frac{2lnx}{{x}^{2}}$,G′(x)=$\frac{2x(1-2lnx)}{{x}^{4}}=0$,⇒x=$\sqrt{e}$.
∴G(x)在($\sqrt{2}$,$\sqrt{e}$)上为增函数,在($\sqrt{e}$,e)上为减函数.
G(x)max=G($\sqrt{e}$)=$\frac{1}{e}$,G(e)=$\frac{2}{{e}^{2}}$<G(2)=$\frac{2ln2}{4}=\frac{ln2}{2}=G(\sqrt{2})$
∴$\frac{ln2}{2}≤a<\frac{1}{e}$,∴a的取值范围为[$\frac{ln2}{2}$,$\frac{1}{e}$)
点评 本题考查了导数的综合应用,转化思想是关键,属于压轴题.


科目:高中数学 来源: 题型:选择题
| 患心脏病 | 患其它病 | 总计 | |
| 秃顶 | 214 | 175 | 389 |
| 不秃顶 | 451 | 597 | 1048 |
| 总计 | 665 | 772 | 1437 |
| A. | 秃顶与患心脏病一定有关系 | |
| B. | 在犯错误的概率不超过0.010的前提下,认为秃顶与患心脏病有关系 | |
| C. | 我们有1%的把握认为秃顶与患心脏病有关系 | |
| D. | 在犯错误的概率不超过0.010的前提下,认为秃顶与患心脏病没有关系 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
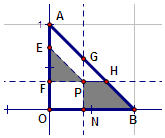 △AOB是直角边长为1的等腰直角三角形,在坐标系中位置如图所示,O为坐标原点,P(a,b)是三角形内任意一点,且满足b=2a,过P点分别做OB,OA,AB三边的平行线,求阴影部分面积的最大值及此时P点坐标.
△AOB是直角边长为1的等腰直角三角形,在坐标系中位置如图所示,O为坐标原点,P(a,b)是三角形内任意一点,且满足b=2a,过P点分别做OB,OA,AB三边的平行线,求阴影部分面积的最大值及此时P点坐标.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{5}$ | B. | $\frac{5}{3}$ | C. | $\frac{4}{5}$ | D. | $\frac{5}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 4 | D. | 8 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com