
正方体 的棱长为
的棱长为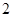 ,
, 是它的内切球的一条弦(我们把球面上任意两点之间的线段称为球的弦),
是它的内切球的一条弦(我们把球面上任意两点之间的线段称为球的弦), 为正方体表面上的动点,当弦
为正方体表面上的动点,当弦 的长度最大时,
的长度最大时,

 的取值范围是 .
的取值范围是 .

解析试题分析:当弦MN经过圆心时,弦MN最长,此时,MN=2,。以A‘为原点,如图,建立空间直角坐标,不妨设MN是上下底面对中心,则M(1,1,2),N(1,1,0),设P(x,y,z),则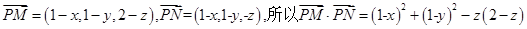 ,因为P为正方体面上的点,根据x,y,z的对称性可知,
,因为P为正方体面上的点,根据x,y,z的对称性可知,

 的取值范围与点P在那个面上无关。不妨设,点P在底面
的取值范围与点P在那个面上无关。不妨设,点P在底面 内,此时有0≤x≤2,0≤y≤2,z=0,所以此时
内,此时有0≤x≤2,0≤y≤2,z=0,所以此时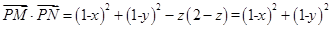 ,当x=y=1时,
,当x=y=1时,

 =0,此时
=0,此时

 最小。当点P位于正方形的顶点时,
最小。当点P位于正方形的顶点时,

 最大,此时有
最大,此时有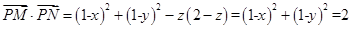 ,所以
,所以

 最大为2.
最大为2.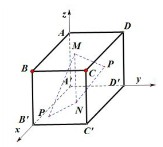
考点:平面向量的数量积;空间直角坐标系。
点评:此题的难度较大,主要考查学生最值的求法,灵活应用空间直角坐标系,设出点的坐标,把几何问题转化为代数问题来解决。


 阅读快车系列答案
阅读快车系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com