[题目]如图.为了测量对岸A.B两点的距离.沿河岸选取C.D两点.测得CD=2km.∠CDB=∠ADB=30°.∠ACD=60°.∠ACB=45°.求A.B两点的距离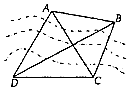．题目和参考答案——青夏教育精英家教网—

【题目】如图，为了测量对岸A，B两点的距离，沿河岸选取C，D两点，测得CD=2km，∠CDB=∠ADB=30°，∠ACD=60°，∠ACB=45°，求A，B两点的距离．

【答案】解：∠DAC=180°﹣∠ADB﹣∠BDC﹣∠ACD=60°，CD=2km
∴AC=2，
∠DBC=180°﹣∠BDC﹣∠ACD﹣∠ACB=45°
在△CDB中由正弦定理得：BC=
在△ABC中由余弦定理得：AB2=CB2+AC2﹣2CBACcos∠ACB=2，
∴AB= km．
答：A、B两点间的距离为 km．
【解析】根据题中条件先分别求出∠DAC，∠DBC．在△ADC中由正弦定理求得AD，在△CDB中由正弦定理求得DB，最后△ADB中由余弦定理求得AB．

练习册系列答案

口算题卡加应用题专项沈阳出版社系列答案

名师伴你成长课时同步学练测系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：

【题目】算法流程图如图所示，则输出的结果是．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】某学校为了解学校食堂的服务情况，随机调查了50名就餐的教师和学生．根据这50名师生对餐厅服务质量进行评分，绘制出了频率分布直方图（如图所示），其中样本数据分组为[40，50），[50，60），…，[90，100]．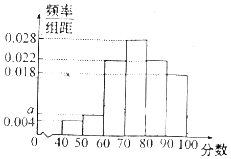
（1）求频率分布直方图中a的值；
（2）从评分在[40，60）的师生中，随机抽取2人，求此人中恰好有1人评分在[40，50）上的概率；
（3）学校规定：师生对食堂服务质量的评分不得低于75分，否则将进行内部整顿，试用组中数据估计该校师生对食堂服务质量评分的平均分，并据此回答食堂是否需要进行内部整顿．