
����Ŀ��ij���еĻ�Ϊ�ֻ�ר����Ը�������ʹ�û�Ϊ�ֻ���������е���.��ʹ�û�Ϊ�ֻ����û��У������ȡ100����������(��λ:�꣩����ͳ�Ƶ�Ƶ�ʷֲ�ֱ��ͼ��ͼ��

��1������Ƶ�ʷֲ�ֱ��ͼ���ֱ����������ƽ������ͬһ�������ø�������е�ֵ������)����λ���Ĺ���ֵ(����ȷ����λ����
��2���ڳ�ȡ����100�������У���������зֲ��������ȡ20�˲μӻ�Ϊ�ֻ���������ٴ���20����������![]() ��
��![]() ����Ⱥ����ѡȡ2�˸�����һ����Ϊ�ֻ�������2���������䶼��
����Ⱥ����ѡȡ2�˸�����һ����Ϊ�ֻ�������2���������䶼��![]() �ڵĸ���.
�ڵĸ���.
���𰸡���1����������2��![]()
����������������1��ֱ������Ƶ�ʷֲ�ֱ��ͼ��ƽ��ֵ����λ����ʽ���.(2)���ùŵ��������2���������䶼��![]() �ڵĸ���.
�ڵĸ���.
��⣺(��) ƽ��ֵ�Ĺ���ֵ:
![]()
![]()
��λ���Ĺ���ֵ��
��Ϊ![]() ��
��![]()
������λ��λ������![]() ������У�����λ��Ϊ
������У�����λ��Ϊ![]() ��
��
����![]() ��
��![]() .
.
(��) �÷ֲ�����ķ�������ȡ��20�ˣ�Ӧ��4��λ��![]() ������ڣ���Ϊ
������ڣ���Ϊ![]() ��2��λ��
��2��λ��![]() ������ڣ���Ϊ
������ڣ���Ϊ![]() .
.
�ִ���6���������ȡ2�ˣ�������¼��ռ�Ϊ![]() ����
����
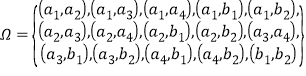
��2���������䶼��![]() Ϊ�¼�A����
Ϊ�¼�A����
![]() ,
,
����![]() .
.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��У��չ���ܴ������ס��������ѡȡ5��ѧ���ӹ�ij���������4��Сʱ��ÿ��ѧ���ӹ��ĺϸ��������ͳ�����ݵľ�Ҷͼ��ͼ��ʾ����֪�װ�ѧ����4��Сʱ�ڼӹ��ĺϸ��������ƽ����Ϊ21���Ұ�ѧ����4��Сʱ�ڼӹ��ĺϸ��������ƽ���������ڼװ��ƽ����.
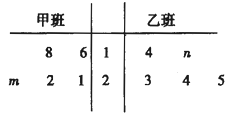
��1����![]() ��ֵ��
��ֵ��
��2���ֱ�����ס�������ѧ����4��Сʱ�ڼӹ��ĺϸ�������ķ���![]() ��
��![]() �����ɴ˱Ƚ�����ѧ���ļӹ�ˮƽ���ȶ���.
�����ɴ˱Ƚ�����ѧ���ļӹ�ˮƽ���ȶ���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������˵����ȷ����( )
�ٺ����Ķ������ֵ��ȷ�������Ķ�Ӧ��ϵҲ��ȷ���ˣ�
��f(x)��![]() �Ǻ�����
�Ǻ�����
�ۺ���y��2x(x��N)��ͼ����һ��ֱ�ߣ�
��f(x)��![]() ��
��![]() ��ͬһ������
��ͬһ������
A.0��B.1��C.2��D.3��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��˾�ƻ�����1̨���������ֻ���ʹ���������̭.�ڹ�������ʱ������һ���Զ����ά����ÿ��ά�������200Ԫ������ʵ��ά��һ�λ�����ά����Ա֧��С�ѣ�С��ÿ��50Ԫ.�ڻ���ʹ���ڼ䣬���ά������������ʱ�����ά�����������ÿά��һ����֧��ά�������500Ԫ������֧��С��.��������ڹ������ʱӦͬʱһ���Թ���ά����Ϊ���Ѽ���������100̨���ֻ���������ʹ�����ڵ�ά������������ͳ�Ʊ���
���� | 8 | 9 | 10 | 11 | 12 |
Ƶ�� | 10 | 20 | 30 | 30 | 10 |
��x��ʾ1̨����������ʹ�����ڵ�ά������y��ʾ1̨������ά��������ķ��ã���λ��Ԫ����![]() ��ʾ������ͬʱ�����ά�������.
��ʾ������ͬʱ�����ά�������.
��1����![]() =10����y��x�ĺ�������ʽ��
=10����y��x�ĺ�������ʽ��
��2����Ҫ��ά����������![]() ����Ƶ�ʲ�С��0.8����n����Сֵ��
����Ƶ�ʲ�С��0.8����n����Сֵ��
��3��������100̨�����ڹ�����ͬʱÿ̨������10��ά����ÿ̨������11��ά���ֱ������100̨������ά����������õ�ƽ�������Դ���Ϊ�������ݣ�����1̨������ͬʱӦ����10�λ���11��ά����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���趨����[��2��2]�ϵĺ���f��x��������[0��2]�ϵ����ݼ�����f��1��m����f��3m����
��1��������f��x��������[��2��2]�����溯������ʵ��m��ȡֵ��Χ��
��2��������f��x��������[��2��2]����ż��������ʵ��m��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1���ȱߡ�ABC�У�AC��4��D�DZ�AC�ϵĵ㣨����A��C�غϣ�������D��DE��BC��AB�ڵ�E����DE����ADE��������ʹ��ƽ��ADE��ƽ��BCDE����ͼ2��ʾ��
��1��������ֱ��BE��AC��ֱ��ȷ��ͼ1�е�D��λ�ã�
��2��֤�������۵�D��λ����Σ������D��AE��B������ֵ��Ϊ��ֵ������������ֵ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������ö�ʵؾ��ȵ�Ӳ�ң����¼�A=����һöӲ�����泯�������¼�B=���ڶ�öӲ�ҷ��泯����.
��1��д�������ռ䣬���о�A��B�����������㣻
��2�����н�������ȷ���ǣ� ��.
A.A��B��Ϊ�����¼� B.A��B���� C.A��B��� D.P��A��=P��B��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������![]() �Ķ�����Ϊ
�Ķ�����Ϊ![]() ���Ҵ���ʵ����
���Ҵ���ʵ����![]() ��ʹ�ö��ڶ�����������
��ʹ�ö��ڶ�����������![]() ������
������![]() ��������ƴ˺���
��������ƴ˺���![]() ���С�����
��������![]() ��.
��.
��1���жϺ���![]() �Ƿ���С�
�Ƿ���С�![]() ���ʡ��������С�
���ʡ��������С�![]() ���ʡ����������
���ʡ����������![]() ��ֵ�ļ��ϣ��������С�
��ֵ�ļ��ϣ��������С�![]() ���ʡ�����˵�����ɣ�
���ʡ�����˵�����ɣ�
��2����֪����![]() ���С�
���С�![]() ���ʡ����ҵ�
���ʡ����ҵ�![]() ʱ��
ʱ��![]() ������
������![]() ������
������![]() �ϵ�ֵ��
�ϵ�ֵ��
��3����֪����![]() �Ⱦ��С�
�Ⱦ��С�![]() ���ʡ����־��С�
���ʡ����־��С�![]() ���ʡ����ҵ�
���ʡ����ҵ�![]() ʱ��
ʱ��![]() ��������
��������![]() ��ͼ����ֱ��
��ͼ����ֱ��![]() ��2017�������㣬��ʵ��
��2017�������㣬��ʵ��![]() ��ֵ.
��ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() ������
������![]() ������
������![]() .
.
��1������![]() ������
������![]() �ϵ����ֵ����Сֵ��
�ϵ����ֵ����Сֵ��
��2����֤�����ڴ���![]() ����ʵ��
����ʵ��![]() ��ʹ�ò���ʽ
��ʹ�ò���ʽ![]() ������
������![]() �н�.������
�н�.������![]() Ϊ��Ȼ�����ĵ�����
Ϊ��Ȼ�����ĵ�����
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com