考点:命题的真假判断与应用
专题:简易逻辑
分析:求出函数的解析式,然后求出数列的和判断①的真假.利用反例判断②的正误;通过特称命题的否定判断③的正误;请查收的三个零点,求出和判断④的正误.
解答:
解:对于①,若f(3
x)=4xlog
23+2=4log
23
x+2,令3
x=t,可得f(t)=4log
2t+2,
则f(2)+f(4)+…+f(2
8)=4log
22+2+8log
22+2+12log
22+2+16log
22+2+20log
22+2+24log
22+2+28log
22+2+32log
22+2=160≠180,所以①不正确.
对于②,函数f(x)=tan2x的对称中心是(
,0)(k∈Z),所以②不正确.
对于③,“?x∈R,x
3-x
2+1≤0”的否定是“?x∈R,x
3-x
2+1>0”;满足特称命题的否定形式,所以③正确.
对于④,设常数a使方程sinx+
cosx=a化为2sin(x+
)=a,在闭区间[0,2π]上恰有三个解x
1=0,x
2=
,x
3=2π,则x
1+x
2+x
3=
.所以④正确.
故选:D.
点评:本题考查命题的真假的判断与应用,可以采用排除法解答,方便快捷,本题考查函数的解析式的求法,命题的否定,函数的零点以及三角函数的对称轴的应用,考查分析问题解决问题的能力.



 名校课堂系列答案
名校课堂系列答案 一个社会调查机构就某地居民的月收入调查了10000人,并根所得数据画了样本的频率分布直方图(如图所示)为了进一步分析居民的收入与年龄、学历、职业等方面的关系,要从这10000人中再用分层抽样方法抽出100人作进一步调查,则在(2500,3000元/月)收入段应抽出( )人.
一个社会调查机构就某地居民的月收入调查了10000人,并根所得数据画了样本的频率分布直方图(如图所示)为了进一步分析居民的收入与年龄、学历、职业等方面的关系,要从这10000人中再用分层抽样方法抽出100人作进一步调查,则在(2500,3000元/月)收入段应抽出( )人.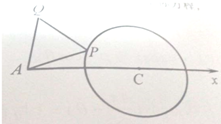 已知半径为2的定圆C外一定点A,且AC=4,在圆上任取一点P,以AP为一边逆时针作等边△APQ,当P在圆上运动时,建立适当的极坐标系,求点Q轨迹的极坐标方程,并转化为直角坐标方程.
已知半径为2的定圆C外一定点A,且AC=4,在圆上任取一点P,以AP为一边逆时针作等边△APQ,当P在圆上运动时,建立适当的极坐标系,求点Q轨迹的极坐标方程,并转化为直角坐标方程.