
| A. | 若$\overrightarrow a•\overrightarrow b=\overrightarrow a•\overrightarrow c$,则$\vec b=\overrightarrow c$ | |
| B. | 若$\overrightarrow a•\overrightarrow b=0$,则$\vec a=\vec 0$或$\vec b=\vec 0$ | |
| C. | 若不平行的两个非零向量$\overrightarrow a,\overrightarrow b$满足$|\overrightarrow a|=|\overrightarrow b|$,则$(\overrightarrow a+\overrightarrow b)•(\overrightarrow a-\overrightarrow b)=0$ | |
| D. | 若$\overrightarrow a$与$\overrightarrow b$平行,则$\overrightarrow a•\overrightarrow b=|\overrightarrow a|•|\overrightarrow b|$ |
分析 利用向量的数量积以及向量的模判断选项即可.
解答 解:对于A,$\overrightarrow a•\overrightarrow b=\overrightarrow a•\overrightarrow c$,如果$\overrightarrow{a}$=$\overrightarrow{0}$,则$\overrightarrow{b}≠\overrightarrow{c}$,也可能$\overrightarrow{b}=\overrightarrow{c}$,所以A不正确;
对于B,若$\overrightarrow a•\overrightarrow b=0$,则$\vec a=\vec 0$或$\vec b=\vec 0$,或$\overrightarrow{a}⊥\overrightarrow{b}$,所以B不正确;
对于C,若不平行的两个非零向量$\overrightarrow a,\overrightarrow b$满足$|\overrightarrow a|=|\overrightarrow b|$,$(\overrightarrow{a}+\overrightarrow{b})(\overrightarrow{a}-\overrightarrow{b})$=${\overrightarrow{a}}^{2}-{\overrightarrow{b}}^{2}$=0,则$(\overrightarrow a+\overrightarrow b)•(\overrightarrow a-\overrightarrow b)=0$
,正确;
对于D,若$\overrightarrow a$与$\overrightarrow b$平行,则$\overrightarrow a•\overrightarrow b=|\overrightarrow a|•|\overrightarrow b|$或$\overrightarrow{a}•\overrightarrow{b}$=-$|\overrightarrow{a}||\overrightarrow{b}|$,所以D不正确.
故选:C,
点评 本题考查命题的真假的判断与应用,向量的数量积以及向量的模的求法,考查转化思想以及计算能力.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ?p:?x∈R,sinx≤1 | B. | ?p:?x∈R,sinx≤1 | C. | ?p:?x∈R,sinx≤1 | D. | ?p:?x∈R,sinx>1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2n-1 | B. | ${(\frac{1}{2})^{n-1}}$ | C. | ${(\frac{2}{3})^{n-1}}$ | D. | ${(\frac{3}{2})^{n-1}}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
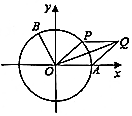 如图,以坐标原点O为圆心的单位圆与x轴正半轴相交于点A,点B、P在单位圆上,且B(-$\frac{\sqrt{5}}{5}$,$\frac{2\sqrt{5}}{5}$),∠AOB=α.
如图,以坐标原点O为圆心的单位圆与x轴正半轴相交于点A,点B、P在单位圆上,且B(-$\frac{\sqrt{5}}{5}$,$\frac{2\sqrt{5}}{5}$),∠AOB=α.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com